В работах [1],[2] проведен термодинамический анализ отопительной системы как структуры диссипативного типа. Здесь субъект представляет натурную модель и внешний вид лабораторно-вычислительного комплекса. Последовательно рассматривает несколько моделей диссипативной термодинамической реальности. Это модельная схемотехническая реальность с ограждающей поверхностью, модель в виде потокового графа учитывающая все потоки энергии, в том числе и диссипативные, термодинамическая структурная модель рассматриваемой энергетической системы теплоснабжения. Субъект при этом понимает, что модель классической термодинамики подразумевает наличие холодного (ХИТ) и горячего (ГИТ) источников теплоты, которые связаны прямой и обратной связями с помощью рабочего тела (РТ). Два разнородных источника теплоты (ЭТГ) и механической (ЭН) энергии в системе питаются электрической энергией. Система разнородная потому, что ее основные блоки связаны между собой рабочим телом(теплоносителем) имеют разное функциональное назначение. Рабочее тело перемещается в тепловой сети по кольцевой системе. За счет источника электрической энергии организован термодинамический цикл с изменением внутренней энергии рабочего тела и с совершением механической работы. В окружающую среду (ОС) уходит теплота от холодного источника и каждого блока системы. Если диссипативные потоки теплоты от блоков уходят в ОС ограниченную ограждающими поверхностями помещения , то учитывается их влияние на параметры микроклимата в нем,рис.1.
Таким образом, субъект иллюстрирует методологическое удобство от использования слагаемых, описывающих свойства "диссипативности и интегральности применения первого и второго законов термодинамики" на примере рассмотрения нескольких термодинамических моделей как объективной, так субъективных реальностей[1,2].
Работа актуальна, поскольку производственные установки с электротепло- гидравлическими преобразователями энергии широко применяются в системах децентрализованного теплотехнологического типа. В связи с их экологической, технико-экономической целесообразностью они получили распространение в местах, где оказываются неконкурентоспособными источники теплоты другой технической организации.
В таких установках для получения теплоты наряду с электрической формой энергии используются энергетические потоки диссипативного типа, которые вызваны турбулентными, вихревыми, кавитационными, электромагнитными эффектами. Считается, что особым образом организованные диссипативные процессы энергии дают возможность использовать полезно «дополнительное количество теплоты при незначительном увеличении входной мощности».[3].Сознательный выбор субъектом тех или иных преимуществ от комбинированного использования энергии требует наличия методики изложения материала связанного с эффективностью тех или иных особенностей диссипативных взаимопревращений энергии неизбежно сопутствующих суммарному и полезному энергопревращениям.
Ввиду сложности процессов сопровождающих энергопревращения в установках электротеплогидравлического типа требуется получение большого объема разнородной экспериментальной и расчетной информации, которая не всегда может быть получена и обработана в одноуровневом иерархическом представлении. Поэтому субъект склонен рассмотреть несколько модельных уровней представления информации.
Из работы [3] следует, что уравнение для расчета «избыточного» диссипативного тепла .активированной жидкости Qизб содержит коэффициент активации жидкости k1
, (1)
где Sв1, Sв2 – удельные энтропии активированной и не активированной жидкости, кДЖ/кг·K; m, μ масса и молярная масса жидкости, кг, кг/моль; T1, Тпл – температуры жидкости на участке активации и после нее в К. Для определения k1 необходимо иметь поля указанных термодинамических параметров до и после активации элементарных объемов рабочего тела. Как правило поля параметров субъект получает экспериментально- расчетным путем.
Системы дифференциальных уравнений с диссипативными слагаемыми в потоках жидкости сформированы в работах Л.Д. Ландау, Л.Г. Лойцянского, А.Н Патрашева[4],[5],[6].
В уравнении (2) (Л.Д. Ландау и Е.М. Лифшиц) первый член в правой части отражает составляющую энтропии от процесса теплопроводности, а остальные два слагаемых обусловлены силами внутреннего трения.
(2)
Л.Г. Лойцянский изменение внутренней энергии
и энтропии 
в потоке несжимаемой вязкой жидкости связывает с притоком тепла pqпоступающего в систему из вне, и потерянной мощности действующих механических внутренних сил(-Nin) (3)
(3)
В (3) величина мощности внутренних сил эквивалентна выделяемой теплоте, существенно положительна, и ее изменение приводит к увеличению потока внутренней энергии и энтропии.
В электро термогидравлических системах, где имеет место нагрев жидкости за счет прямого пропускания электрического тока через воду возникают электромагнитные силы. Воздействие таковых на поток жидкости рассмотрены в работах А.Н Патрашева, Л.И. Седова[7]. Балансовые уравнения энергии гидромеханики уточняются источниками энергии от пондеромоторных G3 электродинамических сил (4). В результате c учетом сил турбулизующих потоки жидкости формируется система дифференциальных уравнений в частных производных (4) – (12).
, (4)
, (5)
, (6)
(7)
(8)
(9)
(10)
. (11)
, (12)
где 
мощность, затрачиваемая на джоулево тепло; W0 - мощность заданных объемных механических сил; 
коэффициенты теплопроводности жидкости;
магнитная проницаемость жидкости;B - магнитная индукция, Тл; 
- изменение энергии среды при включении магнитного поля, 
-совершаемая работа, производимая над токами (источниками магнитного поля) 
, Дж, 
- плотность электрических зарядов, Кл/м3; j – вектор плотности электрического тока, А/м3;
электрическая проводимость жидкости; GЭ- пондемоторная сила, на единицу объема жидкости; 
- градиент давления, Па/м; 
- составляющая характеризующая наличие сил вязкости; G0- внешняя объемная сила механической природы; 
- градиент температуры в элементарном объеме жидкости; 
- изменение энтропии во времени; 
- скорость изменения энтропии в координатном пространстве;
- мощность механических диссипативных сил переходящих в теплоту; 
коэффициенты молекулярной и объемной вязкости;
Значения локальных турбулентных эпюр скоростей 
входят в дифференциальные уравнения турбулентного движения жидкости Фурье-Кирхгоффа вида (9) и Навье - Стокса (10). В систему входят феноменологические коэффициенты в виде коэффициентов турбулентной эффективной теплопроводности 
и вязкости
, которые зависят от профилей температуры 
и скорости 
в пограничных слоях, касательных турбулентных и эффективных механических напряжений 
,
, длины пути перемешивания
(11,12). Упрощенная запись дифференциальных уравнений энергии и движения (9), (10) для турбулентного движения жидкости через значения локальных турбулентных скоростей выведена на основе трех зонной теории турбулентности Л.Прандтля и А.Н.Шерстюка[8],[9], который приспособил ее для цилиндрических каналов.
Система уравнений (1-12) наиболее полно отражают связь между удельным обобщенным энергетическим показателем электротермомеханического состояния теплоносителя (энтропией) и другими параметрами, влияющими на его энергетическое состояние.
В трудах М.П. Вукаловича, И.И. Новикова, А.И. Андрющенко, В.М Бородянского, Д.П. Гохштейна[10],[11],[12],[13], «энтропия» рассматривается как калорический параметр состояния идеальной или реальной равновесной термодинамической системы. В микроуровневом представлении он входит в дифференциальные характеристические уравнения для ряда термодинамических потенциалов, что позволяет вычислять физические свойства веществ. определять эксергетические и энергетические потери в реальных процессах, идущих в теплотехнических установках.
В работах Г.Н. Алексеева [14], описываются особенностях применения энтропии в разнообразных энергетических системах, сформулированы законы энергоэнтропики в явном виде. Применение, которых к анализу нескольких неравновесных термодинамических систем позволяет сравнивать их энергетическое состояние и выбирать оптимальные для работы условия. И.Р. Пригожин[15], сформулировал принцип минимума воспроизводства энтропии для открытых линейных неравновесных термодинамических систем находящихся в стационарных условиях. И. Дьярмати, Р. Шехер [16],[17], удачно использует принцип минимального возникновения энтропии вместе с вариационными методами решения задач гидротермического типа. Я.И. Аснин[18], ввел в обращение энтропийный критерий, который позволяет в сочетании с другими критериями теплообмена обрабатывать большое количество экспериментальных данных. И. Дьярмати вывел уравнения баланса энтропии и показал, что из них можно получать все уравнения гидродинамики, теплообмена и математической физики. Тем самым сделал шаг к утверждению, что неравновесная термодинамика становится наукой имеющей общий мировоззренческий междисциплинарный характер. С.Р.Де Грот, П. Мазур[19], пользуются в своих работах дифференциальными уравнениями баланса и воспроизводства энтропии для изучения процессов переноса массы и энергии. Б.М. Коганович, А.П. Меренков [20],[21], используют понятие энтропии для решения экстремальных задач возникающих в гидравлических сетях. А.В. Лыков и Ю.А. Михайлов[22] широко пользуются энтропийной теоремой теории Онзагера для вывода уравнений тепломассопереноса. Э.Х. Лийв[23], вводит понятие «обобщенной энтропии» для решения не только задач информационного плана, но для различных систем, включая социальные. А.В. Дмитриенко, В.Г. Попов[24] излагают основы феноменологической линейной и нелинейной неравновесной термодинамики, где большое место уделено системному анализу существующих законов неравновесной термодинамики, которая использует при построении своих моделей феноменологические уравнения связанные с теорией энтропии. Они дают формулировку «нелинейной термогидравлической» системы. Показано, что эти системы являются одними из ярких представителей неравновесных систем, в которых сочетаются линейные и нелинейные области , которые сформированы и зависят как от агрегатного состояния рабочего тела, так и от пространственно – временного состояния системы. Приведены выражения для КПД неравновесной термодинамической системы через энтропию. Показано, что воспроизводство энтропии в системе зависит от необратимых процессов теплопроводности, гидродинамического трения и вязкости, скорости перемещения системы, электромагнитного воздействия, химических реакций, лучистого энергообмена, перекрестных эффектов в многокомпонентных системах и т.д. Однако в работах Эткина В.А. [25] энтропия названа «раковой опухолью» 20 века и приводится системное обоснование этого положения. Необратимость реальных процессов по Эткину В.А, связывается с диссипацией энергии (т.е. с потерей способности к совершению упорядоченной работы), она проявляется в скаляризации процесса, т.е. в утрате им векторной природы. Энергоперенос связан с совершением неупорядоченной работы, энергопревращение - с совершением работы упорядоченной.
«Работа» разных систем описана одним выражением для систем механической, термической, электрической, химической и т.п. (в зависимости от природы преодолеваемых сил); внешней или внутренней (в зависимости от того, где возникают эти силы в самой системе или вне ее); полезной или диссипативной (в зависимости от того, чем сопровождается работа - целенаправленным преобразованием энергии или ее рассеянием).
Главную цель, которую ставит перед собой автор создания теории Эткин В.А дать единое изложение фундаментальных основ ряда инженерных и естественных наук с позиций энергодинамики, как обобщенного учения о силах, что является шагом на пути к построению единой теории поля и имеет большое общенаучное, педагогическое и практическое значения.
Признание существования принципов линейной неравновесной феноменологической термодинамики позволяет писать системы уравнений, в которых наряду с экспериментальными (феноменологическими) уравнениями Фурье, Ома, Фика, Дарси-Вейсбаха присутствуют уравнения типа теплопроводности, Навье-Стокса, Фурье-Кирхгоффа и т.д. По И. Дьярмати все эти уравнения входят в аппарат термодинамики необратимых процессов и справедливы для систем, которые находятся недалеко от состояния равновесия.
Обзор литературы позволяет субъекту понимать, что модель нестационарного течения турбулентного потока жидкости осложненного теплообменом и под воздействием электрического поля как минимум описывается двенадцатью дифференциальными уравнениями в частных и обыкновенных производных со своими граничными и начальными условиями, что для описания всех блоков системы следует искать обобщенный удельный энергетический показатель в виде удельной обобщенной энергии(энтропии), который позволит связать между собой входные и выходные параметры системы и построить энергетическое ее пространство состояния. Учитывая тот факт, что энергия является количественной мерой всех (упорядоченных и неупорядоченных, внешних и внутренних, полезных и диссипативных) работ, которые может совершить система.
Для графа указанного на рис 1 и для системы (1-12) формируется функционал (13).
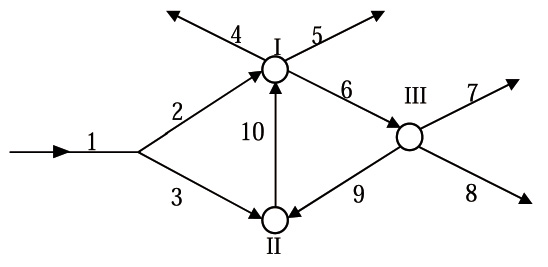
Рис. 1. Граф основных преобразователей ( узлов) и потоков (связей) энергии в электро теплогидравлической системе[1,2]. I – электротеплогенератор (ЭТГ); II – циркуляционный насос(ЭН); III – потребитель; вектора связей - потоки энергии: 1 – электрической энергии из электрической сети; 2 – электрической энергии на тепловыделяющие элементы; 3 –электрической энергии на клеммы насоса; 4–тепловой диссипационной механической энергии внутри теплоносителя; 5 – диссипационной энергии теплоты конвективно-радиационного типа от поверхности теплогенератора; 6 – тепломеханической энергии к потребителю; 7 – теплоотдачи в виде в виде конвективно-радиационного потока от конвекторов; 8 – диссипационных потерь напора на преодоление сопротивлений конвекторов; 9 – тепломеханической энергии к насосу; 10 – тепломеханической формы энергии к электротеплогенератору.
На основе анализа уравнений (1-12), т.е. постановки задачи исследований для обобщенного блока, субъект для процессов идущих в источнике теплоты (ЭТГ) строит функционал (13)
, (13)
который указывает на связи обобщенного интегрального показателя удельной обобщенной энергии (энтропии) с геометрическими, силовыми и потоковыми параметрами исследуемой линейной (нелинейной) диссипативной неравновесной термодинамической системы. Это характерные геометрические размеры ЭТГ, градиенты температур и скоростей, потоки механической и тепловой форм энергии, свойства теплоносителя и металла, время процесса нагрева теплоносителя[27,],[28],[29].
Экспериментально расчетное знание элементов входящих в функционал (13) позволяет вычислить поток удельной обобщенной энергии (энтропии) с использованием феноменологических уравнений Джоуля – Ленца, Ома, Фурье, Дарси, Вейсбаха для любого блока системы и установки в целом.