В экономических исследованиях издавна применяются математические методы, облегчающие решение экономических задач.
Так, знание производной некоторой функции позволяет судить о характерных особенностях в поведении этой функции. Воснове всех таких исследований лежат некоторые теоремы, называемые теоремами о среднем в дифференциальном исчислении. К таким относится теорема Ролля.
Теорема Рóлля (теорема о нуле производной) утверждает, что если функция y = f(x) непрерывная на отрезке [a;b] и дифференцируемая на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
Рассмотрим экономическое применение данной теоремы на примере взаимосвязи предельных затрат со средними затратами.
Для начала раскроем смысл таких понятий как предельные затраты и средние затраты.
Предельные затраты (MC) — показатель предельного анализа производственной деятельности, дополнительные затраты на производство единицы дополнительной продукции. Кривая предельных затрат представлена на рис.1.
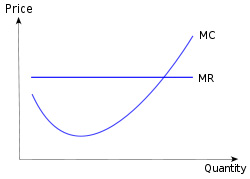
Рис.1
Средние издержки (АТС) представляют собой затраты на единицу выпускаемой продукции. Кривая средних издержек продемонстрирована на рис. 2. Поскольку общие затраты (TC), как правило, состоят из двух слагаемых – постоянных затрат (FC) и переменных затрат (VC), т.е.
TC = FC + VC,
то и средние затраты также можно представить в виде суммы двух слагаемых – средних постоянных затрат (AFC) и средних переменных затрат (AVC), также изображенных на рис. 2:
ATC = AFC + AVC.
Во всех случаях термин «средние затраты» относится к затратам на единицу выпускаемой продукции:
ATC = TC / Q, AFC = FC / Q, AVC = VC / Q.
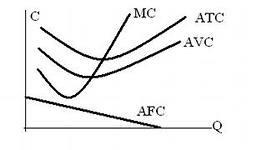
Рис.2
Известно, что кривая предельных затрат (MC) пересекает кривую средних (общих) затрат (АТС) в точке, где средние затраты принимают наименьшее значение. Если график кривой ATC имеет вид, изображенный на рис. 2, т.е. функция ATC(Q) сначала убывает, а потом возрастает, то на отрезке [Q1, Q2] возрастания-убывания, на концах которого
АТС(Q1)=АТС(Q2),в силу теоремы Роллянайдется такая точка Q0, что АТС’(Q0)=0; это стационарная точка функции ATC(Q); следовательно, в этой точке достигается экстремумфункции АТС и в этой точке АТС=МС. (рис.3)
График кривой ATC имеет, как правило, именно такой вид, поскольку этой кривой присуще свойство выпуклости сверху, и поэтому начальное убывание сменяется возрастанием. Это объясняет наличие минимума, а не максимума функции ATC в стационарной точке Q0.
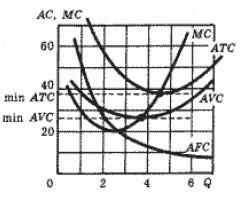
Рис. 3
Совершенно аналогичное поведение присуще функции AVC, что также видно на рис.3.
Можно сделать вывод, что если функция АТС непрерывна на отрезке [Q1;Q2], дифференцируема в интервале (Q1;Q2) и на концах отрезка принимает равное значение: АТС (Q1)=АТС (Q2), то внутри отрезка найдется хотя бы одна точка, в которой производная равна нулю АТС’(Q0)=0; следовательно, в этой точке АТС=МС. То же самое верно и в отношении функции средних пересенных затрат: если функция АVС непрерывна на отрезке [Q1;Q2], дифференцируема в интервале (Q1;Q2) и на концах отрезка принимает равное значение: АVС (Q1)=АVС (Q2), то внутри отрезка найдется хотя бы одна точка, в которой производная равна нулю АVС’ (Q0)=0; следовательно, в этой точке АVС=МС.



