Введение
Данная работа посвящена анализу и моделированию динамики изменения мировых цен на нефтепродукты. Эта задача представляет интерес и актуальна для российской экономики в целом.
В настоящее время большое число экономических исследований проводится с помощью методов корреляционного и регрессионного анализа, которые используются для решения поставленной задачи. Центральной проблемой эконометрики является построение моделей, описывающих реальные экономические процессы, и их дальнейшее использование для построения прогноза. Одной из основных проблем, возникающих в подобных исследованиях является то, что модели оказываются неэффективными для долгосрочного прогноза.
Целью работы является проведение анализа рядов данных, составленных по ежедневным данным котировок Platts мировых цен на нефтепродукты за период с 20.01.2011 по 22.11.2013. По этим данным требуется построить модели, адекватно описывающие динамику рядов, рассчитать точечные и интервальные прогнозы на несколько рабочих дней, оценить точность построенных моделей, сравнивая прогнозные и фактические значения.
Для выполнения работы использовались программные продукты IBM SPSS, Microsoft Excel, а также VSTAT.
Построение модели для динамики цен на дизельное топливо.
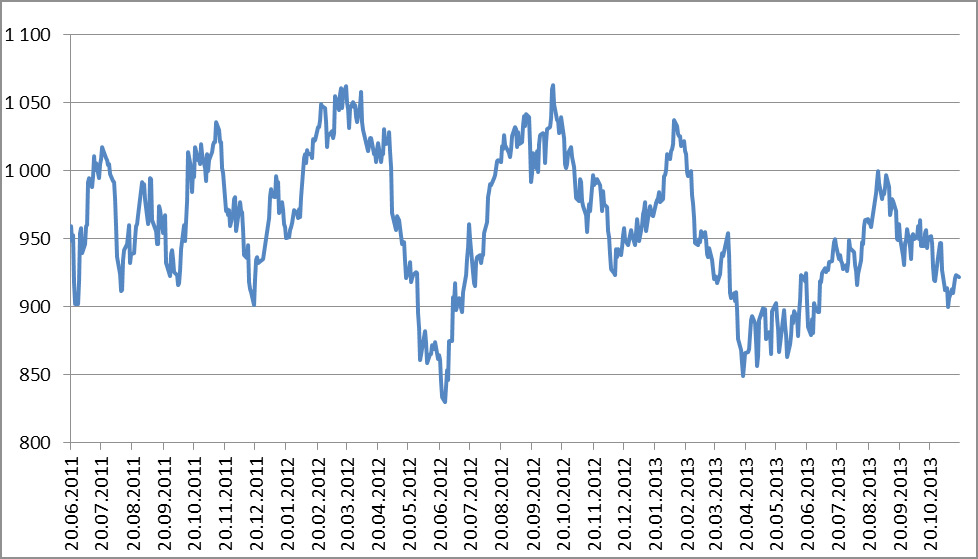
В первую очередь приведем график исходных данных – котировок Platts14 на дизельное топливо. График имеет вид
Platts — независимое информационное агентство США. Является крупнейшим и одним из наиболее уважаемых в мире источником информации об энергетической промышленности, услуг в области маркетинга и компанией, проводящей исследования.
Компания Platts публикует рыночные данные и аналитические материалы, а также эталонные оценки, которые широко используются в качестве ориентиров на физических и фьючерсных рынках.
Для определения ценовых котировок используется информация о совершенных сделках, а также предложения о покупке или продаже товара. В случае отсутствия на рынке ликвидности Platts устанавливает диапазон покупки/продажи на основе консенсуса участников торгов.
Для исследования данных использовались методы анализа временных рядов. Оценка параметров моделей временных рядов и расчет прогнозных значений выполнены с помощью метода авторегрессии проинтегрированного скользящего среднего (АПРСС)2.1
Мультипликативная сезонная АРПСС представляет развитие и обобщение обычной модели АРПСС на ряды, в которых имеется периодическая сезонная компонента. В дополнении к несезонным параметрам (параметры авторегрессии (p), порядок разности (d), параметры скользящего среднего (q)), в модель вводятся сезонные параметры для определенного лага, устанавливаемого на этапе идентификации порядка модели: сезонная авторегрессия (Ps), сезонная разность (Ds) и сезонное скользящее среднее (Qs). Полная сезонная АРПСС записывается как АРПСС (p, d, q) (Ps, Ds, Qs).
Прежде чем оценивать параметры, надо определить их количество, т.е. выбрать модель АРПСС. Для идентификации используют автокорреляционные и частные автокорреляционные функции.
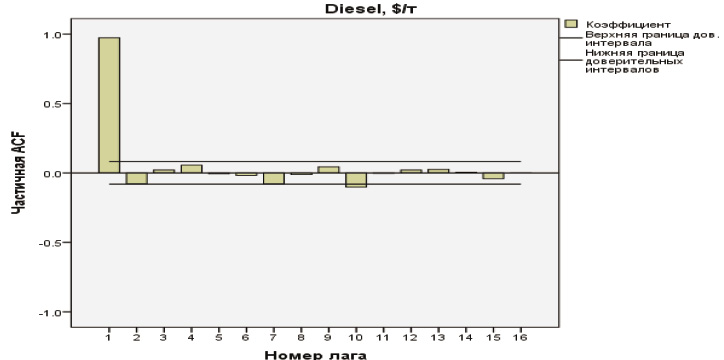
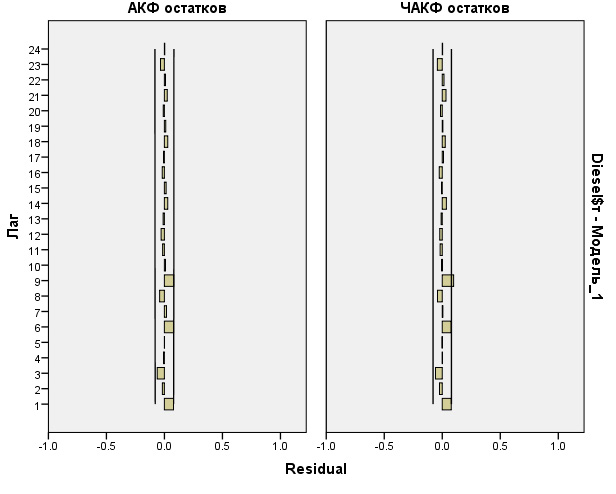
Отобразим автокорреляционные и частные автокорреляционные функции.
Полученные корреллограммы имеют следующий вид:
При построении модели АРПСС в первую очередь необходимо проверить рассматриваемый ряд на стационарность. Признаками нестационарности являются: наличие тренда, гетероскедастичность, изменяющаяся автокорреляция. График АКФ (ACF), позволяет предположить, что это авторегресионный процесс с коэффициентом b1 близким к 1, т.е. нестационарный процесс, поскольку АКФ убывает очень медленно.
Таким образом, для того, чтобы избавиться от не стационарности, при выборе модели данные будут преобразованы с помощью натурального логарифма.
Рассмотрев конфигурацию графиков АКФ и ЧАКФ выберем параметры модели:
Один параметр (p): АКФ - экспоненциально убывает; ЧАКФ - имеет резко выделяющееся значение для лага 1, нет корреляций на других лагах.
Два параметра авторегрессии (p): АКФ имеет форму синусоиды или экспоненциально убывает; ЧАКФ имеет резко выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах.
Один параметр скользящего среднего (q): АКФ имеет резко выделяющееся значение на лаге 1, нет корреляций на других лагах. ЧАКФ экспоненциально убывает.
Два параметра скользящего среднего (q): АКФ имеет резко выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах. ЧАКФ имеет форму синусоиды или экспоненциально убывает.
Один параметр авторегрессии (p) и один параметр скользящего среднего (q): АКФ экспоненциально убывает с лага 1; ЧАКФ - экспоненциально убывает с лага 1.
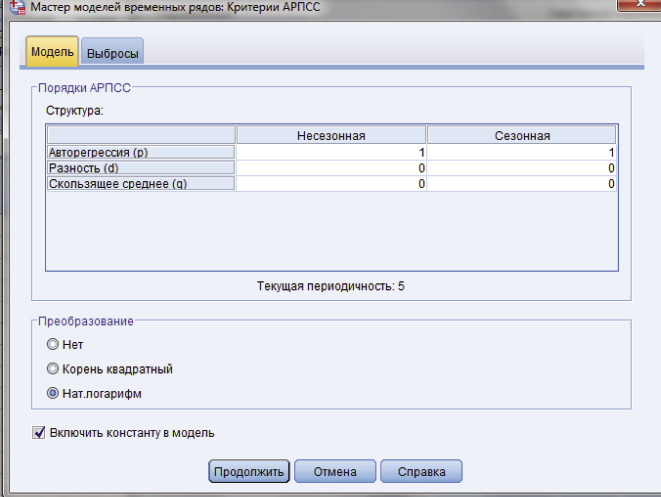
Получившуюся модель можно записать с помощью уравнения
![]()
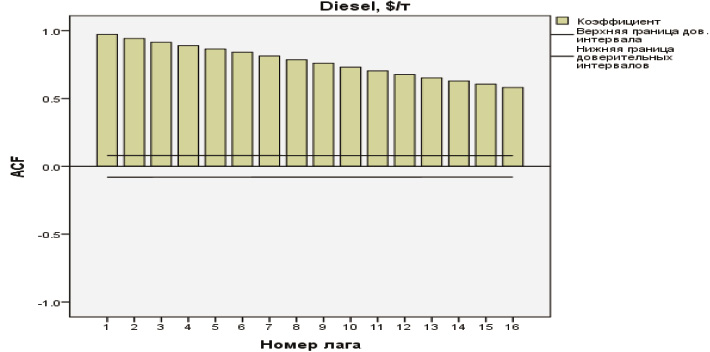
Получившаяся модель имеет следующие характеристики (по расчетам VSTAT3);1
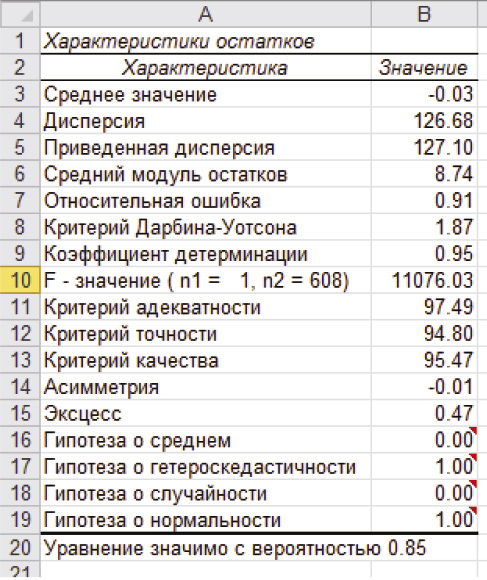
Коэффициент детерминации имеет очень высокое значение R2 = 0,95, следовательно, модель на 95% точно описывает ряд, и всего 5% приходится на ошибку. Значение F-распределения для данной модели равно 11076,03, что больше табличного значения 3,857, следовательно, построенная модель адеквтна. Критерии адекватности, точности и качества модели имеют высокие значения. Коэффициент Дарбина-Уотсона близок к 2, что указывает на отсутствие автокорреляции остатков.
Проанализируем качество модели в программе SPSS4.2[4]
13 Официальный сайт http://www.v-stat.ru/. VSTAT – это программа анализа и прогнозирования данных, работающая в среде Windows 2000/XP/Vista/7 под управлением электронной таблицы MS EXCEL 2003/2007/2010, включающая в себя открытый VBA-код и динамическую библиотеку функций (вычислительное ядро).
24 Официальный сайт http://www-01.ibm.com/software/analytics/spss/ SPSS (аббревиатура англ. «Statistical Package for the Social Sciences», «статистический пакет для социальных наук») — компьютерная программа для статистической обработки данных, один из лидеров рынка в области коммерческих статистических продуктов, предназначенных для проведения прикладных исследований в социальных науках.
Качество подгонки модели в соответствии с SPSS:
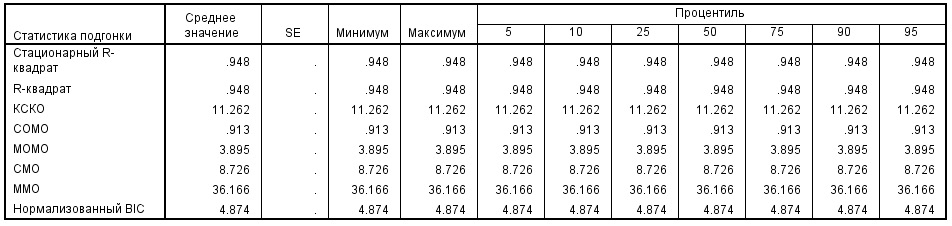
• R-квадрат близок к 1.
• КСКО. Корень среднего квадрата ошибки. Мера того, насколько зависимый ряд отличается от ряда его значений, предсказанных моделью, выраженная в тех же единицах, что и зависимый ряд.
• СОМО. Средний относительный модуль ошибки. Мера того, насколько ряд отличается от ряда его значений, предсказанных моделью. Она не зависит от используемых единиц измерения и поэтому может использоваться для сравнения рядов с разными единицами измерения.
• СМО. Средний модуль ошибки. Мера того, насколько ряд отличается от ряда его значений, предсказанных моделью. СМО представляется в исходных единицах измерения ряда.
• МОМО. Максимальный относительный модуль ошибки. Наибольшая ошибка предсказания, выраженная в процентах. Эта мера полезна, чтобы представить, каким может быть наихудший прогноз.
• ММО. Максимальный модуль ошибки. Наибольшая ошибка прогноза, выраженная в тех же единицах измерения, что и зависимый ряд. Как и МОМО, этот показатель полезен, чтобы представить наихудший вариант прогноза.
• Нормализованный BIC. Нормализованный Байесовский Информационный критерий. Обычная мера общего согласия модели, которая пытается учесть сложность модели. Это значение, основанное на среднем квадрате ошибке, включает штраф за большое число параметров при недостаточной длине ряда. Этот штраф лишает преимущества модели с большим числом параметров, позволяя с помощью данной статистики легко сравнивать разные модели для одних и тех же рядов.
Исходный ряд приведен к стационарному взятием натурального логарифма. Внешний вид АКФ и ЧАКФ дают основание предположить, что рассматриваемый ряд можно описать моделью АРПСС (1 0 0) (1 0 0).
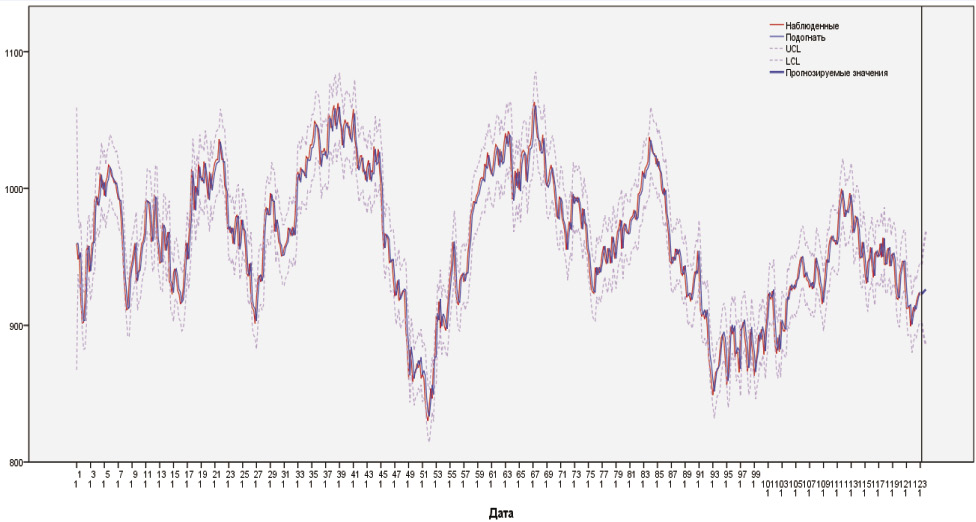
Прогнозные значения модели имеют следующий вид:
Реальные наблюдения последних четырех дней имеют следующие значения:
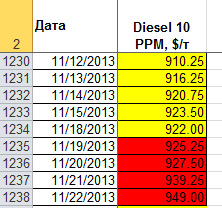
Сравнивая полученные прогнозные значения с фактическими данными, можно заметить, что прогноз продолжает общую возрастающую тенденцию ряда, но достаточно сильно отличается от фактических данных, что не удивительно: построение модели не является эффективным для долгосрочного прогноза цен на нефтепродукты. Наиболее точным является прогноз на первый день.
Фактические данные принадлежат доверительным интервалам.
Заключение
Итак, в данной работе проведен анализ ряда цен на дизельное топливо, составленного по данным котировок Platts за период с 20.01.2011 по 22.11.2013. В процессе решения поставленной задачи была простроена авторегрессионная модель АРПСС (1, 0, 0) (1, 0, 0).
Прогнозные значения на 4 дня, рассчитанные с помощью данной модели, дали неоднозначный результат. Модель оказалась неэффективна для долгосрочного прогноза. Исходя из полученных результатов, можно сделать вывод о том, что динамика цен на нефтепродукты практически непредсказуема, но построенную модель можно использовать для краткосрочного прогноза на 1 день.
Неточность полученных результатов можно объяснить тем, что, во-первых, выбранная модель является адаптивной и опирается на последнее значение ряда данных, а, во-вторых, тенденции рассматриваемого ряда часто нарушаются резкими скачками, обусловленными различными экономическими факторами, которые не учитываются в данном исследовании.
12 Модели АРПСС – класс универсальных линейных моделей для описания стационарных и нестационарных временных рядов. Разработчики – G. P. Box, G.M. Jenkins. Для моделирования используются только данные временного ряда.



