В статье рассматривается модель определения периода времени эффективного вложения капитала в металлургической отрасли РФ. Автор с помощью экономико-математических методов исследует чистый приведенный доход инновационно-инвестиционного цикла. Модель носит универсальный характер и может использоваться в различных отраслях экономики.
The article considers the model of the time period of effective capital investment in the metallurgical industry in Russia Federation. The author investigates the net present value of innovation and investment circle by using economic and mathematical methods. The model is universal and can be used in different sectors of economy.
Россия на сегодняшний день является страной, стабильность которой целиком и полностью зависит от цен на энергоресурсы. Исследования ведущих специалистов Российской академии наук показывают, что в последние годы Российская Федерация существенно отставала от развитых стран по объемам промышленного производства и производительности труда. Это связано с тем, что физический и моральный износ основных средств производства достиг критического уровня (от 65 до 75%), а выбытие основных фондов идет с темпом 1,5-2,5% в год, тогда как годовой темп обновления технологической базы не превышает 0,1-0,5%1. При этом удельный вес производств, соответствующих 5-ому технологическому укладу, возникшему в развитых странах в 90-е годы, сегодня в России составляет лишь 8%, в то время как индустриально развитые страны ведут активную работу по внедрению 6-ого технологического уклада, где инновационный продукт будет значительно опережать добывающие отрасли.
Все это порождает замкнутый порочный круг проблем: изношенные фонды - низкое качество выпускаемой продукции - низкая конкурентоспособность - низкие объемы продаж - недостаточные обороты по финансам - нехватка денежных средств на обновление оборудования. И как следствие, отсутствие возможностей не только для инноваций, но и для сохранения темпов роста производства на достаточно высоком уровне.
В этой связи Правительство РФ уделяет большое внимание процессам модернизации. В частности в своем обращении к Федеральному Собранию Д. Медведев отметил следующее: «В XXI веке нашей стране вновь необходима всесторонняя модернизация, и это будет первый в нашей истории опыт модернизации, основанный на ценностях и институтах демократии. Престиж Отечества и национальное благосостояние не могут до бесконечности определяться достижениями прошлого» 2.
На сегодняшний день во всесторонней структурной модернизации, как в техническом, так и в технологическом плане нуждается большинство отраслей российской экономики, способных обеспечить внутренний рынок. К таким отраслям, прежде всего, относится металлургическая отрасль, являющиеся основой индустриальной мощи экономики любой страны.
Таким образом, особенностью текущего этапа экономического развития является необходимость модернизации металлургической отрасли и ее переориентация на выпуск инновационной продукции. Инновации при этом рассматриваются как основной фактор модернизации экономики, способный обеспечить устойчивый рост с ориентацией на выпуск высокотехнологичной продукции. Реализация этой задачи становится возможной при анализе и прогнозировании показателей оценки экономической эффективности инвестиционных проектов. Поэтому тема данного исследования является актуальной для российской экономики.
Целью настоящего исследования являлось построение модели определение периода эффективного вложения капитала, которая показывает когда необходимо вкладывать денежные средства в обновление основных средств, так чтобы в будущем получить максимальную отдачу от инвестирования или максимальный чистый приведенный доход.
Модель была построена на примере металлургической отрасли, так как она является базовой отраслью экономики России и вносит значительный вклад в прирост ВВП и других макроэкономических показателей. Так на 2010 год доля металлургической промышленности в ВВП страны составляла около 5 %, промышленном производстве порядка 18%, экспорте – 14 %3.
Модель имеет следующие допущения:
1. Ставка дисконтирования d находится как сумма ставки рефинансирования, которая была равна 8% на момент проведения исследования, и риска, связанного с осуществлением инвестиционной деятельности в металлургической отрасли 10%:
![]() 4.
4.
2. Точка максимума (![]() ) первого инновационно-инвестиционного цикла (первой волны) лежит на середине подъема второго инновационно-инвестиционного цикла (второй волны) и для второй волны характерны темпы прироста первой волны на данном отрезке;
) первого инновационно-инвестиционного цикла (первой волны) лежит на середине подъема второго инновационно-инвестиционного цикла (второй волны) и для второй волны характерны темпы прироста первой волны на данном отрезке;
3. Вторая волна имеет такой же вид функциональной зависимости изменения NPV от времени, как и первая.
В модели были использованы следующие обозначения: x – коэффициент соответствующий i–ому году, y – чистый приведенный доход i–ого года. За начало координат принят 2005 год (x=0), тогда 2005+(n+1) году соответствует коэффициент, вычисляемый по формуле 1
x = n + 1, (1)
а 2005-(n+1) году, вычисляемый по формуле 2
x = n – 1. (2)
Первый этап исследования заключался в построении графика зависимости чистого приведенного дохода от времени первого инновационно-инвестиционного цикла. Для этого на основе имеющихся статистических данных был рассчитан NPV проекта по формуле (2):
![]() , (2)
, (2)
где ![]() - объем отгруженных товаров металлургической отрасли;
- объем отгруженных товаров металлургической отрасли;
![]() - затраты на производство и продажу продукции металлургической отрасли;
- затраты на производство и продажу продукции металлургической отрасли;
![]() - инвестиции в металлургическую отрасль;
- инвестиции в металлургическую отрасль;
d - ставка дисконтирования;
t - период времени, соответствующий определенному году.
Расчеты представлены в таблице 1:
Таблица 1
Денежные средства первой волны
|
Год |
№ |
Объем отгруженных товаров, млн.руб. |
Затраты на производство и продажу продукции, млн.руб. |
Инвестиции, млн.руб. |
NPV |
|
2005 |
0 |
1902898 |
1428935 |
-137200 |
336763 |
|
2006 |
1 |
2415858 |
1705749 |
-174400 |
790753,7 |
|
2007 |
2 |
2953135 |
2087187 |
-205600 |
1265005 |
|
2008 |
3 |
3294771 |
2560501 |
-290100 |
1535341 |
|
2009 |
4 |
2393232 |
1924862 |
-246800 |
1649624 |
С помощью модели кривых роста была проанализирована тенденция изменения NPV и оценена ее достоверность с помощью ошибки аппроксимации.
В результате было выявлено, что наиболее подходящей является полином второй степени (парабола) с наименьшей ошибкой равной 3,36%
![]() .
.
Далее с помощью найденной функциональной зависимости были спрогнозированы значения NPV до 2020 года и проведен ретроспективный анализ до 2000 года (табл.2).
Таблица 2
Чистый приведенный доход первой волны
|
Год |
№ |
NPV |
Год |
№ |
NPV |
Год |
№ |
NPV |
Год |
№ |
NPV |
|
2000 |
-5 |
-4209187 |
2004 |
-1 |
-337261 |
2013 |
8 |
992451,4 |
2017 |
12 |
-1697508 |
|
2001 |
-4 |
-3051920 |
2010 |
5 |
1684925 |
2014 |
9 |
509246,7 |
2018 |
13 |
-2685473 |
|
2002 |
-3 |
-2020844 |
2011 |
6 |
1580291 |
2015 |
10 |
-100148 |
2019 |
14 |
-3799629 |
|
2003 |
-2 |
-1115957 |
2012 |
7 |
1349466 |
2016 |
11 |
-835733 |
2020 |
15 |
-5039974 |
Также было найдено максимальное значение NPV, приходящееся на 2010 год и равное 1684925 млн. руб., и, следовательно, момент времени, после которого доход начинает уменьшаться (рис.1).
Второй этап исследования заключался в моделировании второго инновационно-инвестиционного цикла. Для этого были определены темпы прироста чистого приведенного дохода первой волны по формуле (3):
![]() , (3)
, (3)
где ![]() - темп прироста;
- темп прироста;
![]() - уровень сравниваемого периода;
- уровень сравниваемого периода;
![]() - уровень предшествующего периода.
- уровень предшествующего периода.
Рис. 1. NVP первого инновационно-инвестиционного проекта
Найденные темпы прироста NPV представлены в таблице 3.
В стратегии развития металлургической отрасли до 2020 года определены коэффициенты обновления основных фондов - 4% в 2011 году и 5,5% в 2020 году5. 1Данные коэффициенты показывают, какую часть от имеющихся на конец отчетного периода основных средств составляют новые основные средства.
В данном исследовании эти значения были приняты за узловые точки, с помощью которых методом наименьших квадратов было найдено уравнение изменения коэффициента обновления основных средств во времени, равное ![]() .
.
Подставив соответствующий год в найденную функциональную зависимость, были найдены значения остальных коэффициентов обновления основных средств, ![]() (табл. 3).
(табл. 3).
15 Стратегия развития металлургической промышленности России на период до 2020 года. - Министерство промышленности и торговли РФ [Электронный ресурс]. - Режим доступа: http://v2009.minprom.gov.ru/activity/metal/ strateg/2/print
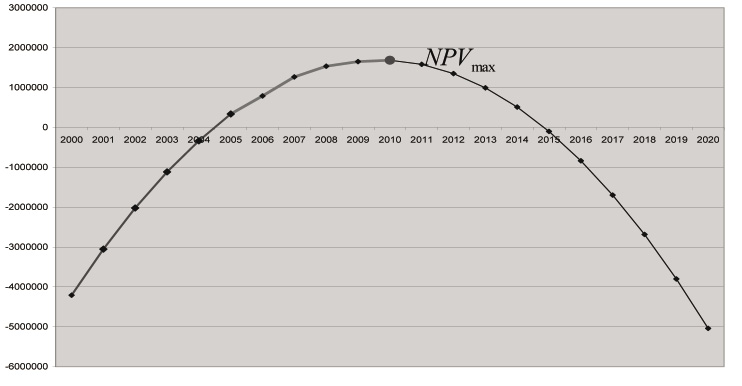
Таблица 3
Увеличенные на величину коэффициента обновления основных средств темпы прироста чистого приведенного дохода первой волны
|
Год |
|
|
|
Год |
|
|
|
|
2000 |
- |
2,15% |
- |
2011 |
-6,21% |
4,00% |
-2,21% |
|
2001 |
-27,49% |
2,31% |
-29,81% |
2012 |
-14,61% |
4,17% |
-10,44% |
|
2002 |
-33,78% |
2,48% |
-36,26% |
2013 |
-26,46% |
4,33% |
-22,12% |
|
2003 |
-44,78% |
2,65% |
-47,42% |
2014 |
-48,69% |
4,50% |
-44,19% |
|
2004 |
-69,78% |
2,81% |
-72,59% |
2015 |
-119,67% |
4,67% |
-115,00% |
|
2005 |
-199,85% |
2,98% |
-202,83% |
2016 |
734,50% |
4,83% |
739,33% |
|
2006 |
134,81% |
3,15% |
137,96% |
2017 |
103,12% |
5,00% |
108,12% |
|
2007 |
59,97% |
3,31% |
63,29% |
2018 |
58,20% |
5,17% |
63,37% |
|
2008 |
21,37% |
3,48% |
24,85% |
2019 |
41,49% |
5,33% |
46,82% |
|
2009 |
7,44% |
3,65% |
11,09% |
2020 |
32,64% |
5,50% |
38,14% |
|
2010 |
2,14% |
3,81% |
5,95% |
Так как второй инновацинно-инвестиционный цикл основан на внедрении новой технологии, значения темпов прироста первой волны были увеличены на величину коэффициента обновления основных средств (учитывая допущение 2) (табл. 3). Заметим, что на первом этапе проекта (первая середина подъема волны до 2005 г.) коэффициент обновления основных средств необходимо было отнимать.
Для середины подъема первой волны характерен темп прироста, равный -202,83%. Зная его и значение NPV в точке максимума, была найдена величина NPV второй волны двух предшествующих и двух последующих лет по формуле (2) (табл.4).
Таблица 4
Темпы прироста чистого приведенного дохода второй волны
|
Год |
NPV |
|
Год |
NPV |
|
|
2008 |
-5978167 |
-47,42% |
2011 |
4009394 |
137,96% |
|
2009 |
-1638516 |
-72,59% |
2012 |
6546858 |
63,29% |
|
2010 |
1684925 |
-202,83% |
Учитывая допущение 3, с помощью метода наименьших квадратов были найдены параметры функциональной зависимости второй волны
![]()
и оценена ее достоверность (ошибка равна 5,73%).
На основе ранее найденной закономерности были вычислены значения NPV для второй волны с 2005 по 2007 гг. и с 2013 по 2024 гг. (табл. 5):
Таблица 5
Значение чистого приведенного дохода второй волны
|
Год |
№ |
NPV |
Год |
№ |
NPV |
Год |
№ |
NPV |
Год |
№ |
NPV |
|
2005 |
0 |
-21986722 |
2013 |
8 |
7832613 |
2017 |
12 |
6959377 |
2022 |
17 |
-8928640 |
|
2006 |
1 |
-15957632 |
2014 |
9 |
8600735,4 |
2018 |
13 |
5097015,6 |
2023 |
18 |
-14079106 |
|
2007 |
2 |
-10586163 |
2015 |
10 |
8711236,9 |
2019 |
14 |
2577033,2 |
2024 |
19 |
-19887194 |
|
... |
… |
… |
2016 |
11 |
8164117,5 |
2020 |
15 |
-600570,2 |
Полученные данные отражены на графике (рис. 2)
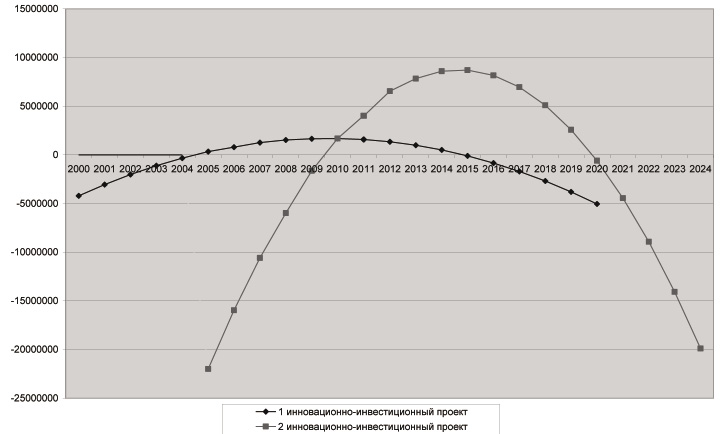
Рис. 2. Первый и второй инновационно-инвестиционный цикл
Таким образом, проведенное исследование позволяет сделать следующие выводы:
• размер инвестиций зависит от года принятия решения (табл. 6).
Таблица 6
Величина инвестиций в инновационные технологии
|
Год |
NPV, млн. руб. |
|
Год |
NPV, млн. руб. |
|
|
2005 |
-21986722 |
21986722,26 |
2008 |
-5978167,187 |
7571083,87 |
|
2006 |
-15957632 |
7114326,59 |
2009 |
-1638515,948 |
8413619,31 |
|
2007 |
-10586163 |
7479233,93 |
• инвестор для сохранения эффективной отдачи от вложенных денежных средств должен был в период 2005-2009 годов принять решение об инвестировании в инновационные технологии следующего технологического уклада;
• на сегодняшний день, для того чтобы уменьшить потери дохода от вложенных средств и совсем не уйти в убыток после 2015 года, инвестору необходимо как можно скорее вкладывать денежные средства в воспроизводство основного капитала.
Как результат проделанной работы, была разработана модель определения периода времени эффективного вложения капитала. Данная модель носит универсальный характер и может использоваться в различных отраслях экономики. Ее применение позволяет определить период времени, когда необходимо вкладывать денежные средства в следующий инновационно-инвестиционный цикл, чтобы предотвратить уменьшение чистого приведенного дохода.



