Поставим задачу провести количественную оценку взаимосвязей показателей с целью получения обоснованных экономических выводов о величине Валового регионального продукта в том или ином регионе.
Валовой региональный продукт (ВРП) – показатель, измеряющий валовую добавленную стоимость, исчисляемый путем исключения из суммарной валовой продукции объемов ее промежуточного потребления, определяется как сумма вновь созданных стоимостей отраслей экономики региона.
Таким образом, Валовой региональный продукт (ВРП) – обобщающий показатель экономической деятельности региона, характеризующий процесс производства товаров и услуг.
Исходными данными для анализа являлись данные о регионах за 2012 г. [3]:
- Площадь территории тыс. км2
- Численность населения на 1 января 2013 г., тыс. человек
- Среднегодовая численность занятых в экономике, тыс. чел.
- Среднедушевые денежные доходы в мес. руб.
- Потребительские расходы в среднем на душу населения (в месяц), руб.
- Среднемесячная номинальная начисленная з/п работников организации.
Первоначально был проведен корреляционный анализ. В результате этого анализа сразу был исключен фактор «Площадь территории тыс. км2», так как ВРП имеет очень низкую парную корреляцию с этой переменной (далее ее не будем рассматривать), что вполне объяснимо, так как площадь территории на практике не всегда сильно влияет на ВРП. При этом имеет место быть мультиколлинеарность, так как есть коэффициенты превышающие значение 0,8 [1].
Матрица коэффициентов парной корреляции
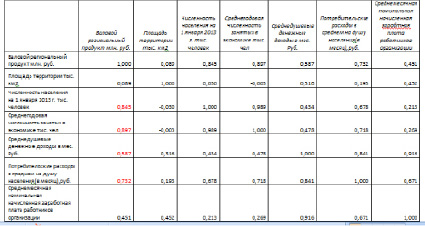
Для выявления мультиколлинеарности факторов был выполнен тест Фаррара-Глоубера [1, c. 213 ] по всем факторам, кроме «Площади территории», в результате которого осталось три фактора: «Численность занятых в экономике», «Потребительские расходы», «Среднемесячная номинальная начисленная заработная плата работников организации».
Продолжая отбирать наиболее значимые факторы в модель множественной регрессии, мы решили произвести пошаговый отбор факторов методом исключения из модели статистически незначимых переменных. в результате пошагового отбора получено трехфакторное уравнение регрессии, все коэффициенты которого (кроме свободного члена) значимы при 5 %-м уровне значимости, вида
y=–1141913+1142,819х1+30,82х2
y – ВРП; x1 – «Среднегодовая численность занятых в экономике»; x2 – «Среднемесячная номинальная начисленная заработная плата работников организации».
Итоговая регрессионная статистика выглядит следующим образом:
|
Регрессионная статистика |
|
|
Множественный R |
0,923323931 |
|
R-квадрат |
0,852527081 |
|
Нормированный R-квадрат |
0,848252504 |
|
Стандартная ошибка |
498979,946 |
|
Наблюдения |
72 |
Говоря о качестве модели, нужно обратить внимание на то что показатель коэффициента детерминации довольно высокий 0,85, коэффициент множественной корреляции показывает, что на 92 % вариации зависимой переменной «ВРП» учтено в модели и обусловлено влиянием включенных факторов. Поэтому мы можем полагаться на достаточно высокую тесноту связи модели.
Для дополнительной проверки модели на значимость, мы использовали критерий Фишера. Согласно расчетам:
Fрасч= 199,44;
Fтабл= 3,14.
Таким образом, мы определяем уравнение регрессии как значимое, так как Fрасч>Fтабл, значит уравнение можно использовать для целей прогнозирования.
Также мы признаем коэффициенты уравнения регрессии значимыми, так как:
Р-значение t-статистика Стьюдента для коэффициентов меньше чем уровень значимости 0.05
Доверительные интервалы не содержат ноль внутри себя – имеют одинаковые знаки
Учитывая, что коэффициенты регрессии невозможно использовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения и разной колеблемости факторов, нами были проанализированы коэффициенты эластичности, бета-коэффициенты, дельта-коэффициенты [1],[2].
Коэффициенты эластичности Эх1=1,67 и Эх2=1,23 показывают, что изменение Y по каждому из факторов эластично, наибольшей эластичностью обладает Y по фактору х1.
Бета-коэффициенты показывают, что при изменении каждого из факторов на одно СКО(среднеквадратического отклонения) ВРП меняется соответственно на 0,836 (обратная связь с первым фактором), 0.226 своего СКО.
Дельта-коэффициенты показывают, что доля влияния фактора Х1(0,88 против 0,12) в совокупном влиянии двух факторов преобладает.
Таким образом, была построена модель регрессии, в которой наибольшее влияние на величину ВРП оказывает фактор «Среднегодовая численность занятых в экономике»
y=–1141913+1142,819x1+30,82x2.
Экономический смысл коэффициентов уравнения: при увеличении численности занятых в экономике на 1 человека ВРП будет увеличиваться на 1142,819 рублей; при увеличении начисленной заработной платы на 1 рубль ВРП будет увеличиваться на 30,82 рублей.



