При оптимизации технического решения часто сталкиваются с тем, что необходимо определить критерии и их влияние на конечное решение. Оптимизация технического решения пьезоактюатора может быть формально описана.
Пьезоактюатор выглядит следующим образом (рис. 1).
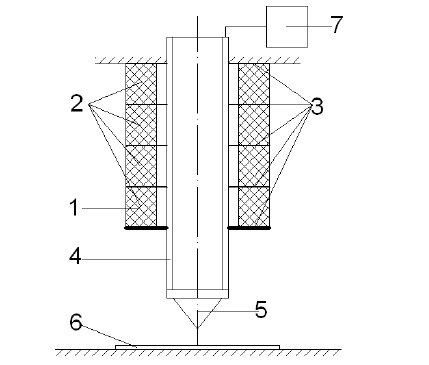
Рис.1. Пьезоактюатор
с системой терморегуляции.
Пьезоактюатор с системой терморегуляцией содержит пьезопривод 1, выполненный из набора пьезоколец 2, между которыми расположены металлические кольца 3, тепловую трубку 4, закрепленную на свободном торце пьезопривода 1, зонд 5, установленный в тепловой трубке 4 и взаимодействующий с подложкой 6, тепловая трубка 4 связана с источником жидкого азота 7.
Устройство наноперемещений зонда работает следующим образом.
При подаче напряжения на металлические кольца 3, происходит механическая деформация пьезопривода 1 из набора пьезоколец 2 вследствие обратного пьезоэффекта, при этом тепловая трубка 4, жестко связанная со свободным торцем пьезопривода 1, выполняет перемещение зонда 5 перпендикулярно подложке 6, в результате сил электрического взаимодействия зонда 5 и подложки 6 выполняется технологический процесс, при этом тепло из рабочей зоны зонда 5 тепловой трубки 4 к источнику жидкого азота 7.
Для начала необходимо определить обобщенный критерий, он будет включать в себя функциональные, экологические и экономические локальные критерии. Подробно опишем каждый из них.
Функциональные критерии: погрешность перемещения, быстродействие, виброустойчивость, термоустойчивость.
Экологические критерии: газовый поток.
Экономические критерии: стоимость и окупаемость.
Имея представление об обобщенном критерии, можно представить процесс потери качества пьезоактюатором с помощью математических выражений. Пусть Х1, Х2, ... Хк будут параметрами, которые определяют состояние пьезоактюатора и одновременно являются функциями времени. Если Х принадлежит множеству состояний GX, то можно говорить о работоспособности устройства. Неработоспособно устройство в том случае, когда все значения Хк больше соответствующих им допустимых значений Хкр. В случае, если некоторые значения превышают допустимые, а некоторые – нет, то пьезоактюатор является частично работоспособным. Параметры качества пьезоактюатора должны подчиняться неравенству Хк ≤ Хкр. Это соответствует тому, что Gх является подмножеством Gхр. Запас по качеству можно описать выражением: Ki = XiP/Xi. В числителе находится нормирующий параметр, в знаменателе – параметр пьезоактюатора. Качество по погрешности перемещения – К1=δр/δ, качество по быстродействию – К2=τр/ τ, качество по газовому потоку – К3=qр/q, по стоимости – К4 = ср/с, по окупаемости – К5 = ор/о , по виброустойчивости – К6= vp/v, по термоустойчивости К7 = Тр/Т. Здесь δp, τp, qp, cp, op, vp, Tp – допустимые значения погрешности перемещения, быстродействия, газового потока, стоимости и окупаемости для пьезоактюатора. δ, τ, q, c, о, v, T – фактические значения величин для пьезоактюатора.
В итоге обобщенный критерий качества выглядит следующим образом:
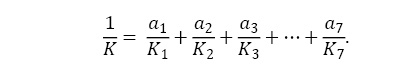
где ai (i от 1 до 7) – весовые коэффициенты, для нахождения которых используется метод экспертных оценок из теории принятия решений.
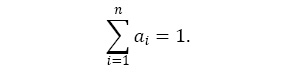
В общем случае:
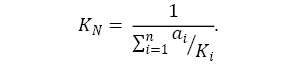
Для дальнейшего анализа технического решения пьезоактюатора применим метод наискорейшего спуска. Градиент является направлением наискорейшего возрастания функции, следовательно, противоположное направление является направлением наискорейшего убывания функции.
Предположим, что происходит перемещение из точки х в точку х + hd, где d – направление, h – шаг некоторой длины. Следовательно, происходит перемещение из точки (х1, ..., хn) в точку (х1+δх1, ..., хn+δхn), где δхi = hdi, хi є Х є Gx. di – косинусы направления d, причем
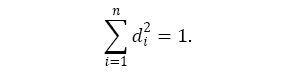
Изменение значений функции определяет соотношение с точностью до первого порядка:
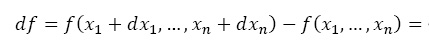
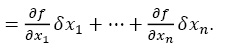
Частные производные вычисляются в точке x. Чтобы получить наибольшее значение изменения функции df для выбора направления di, необходимо решить задачу максимизации с ограничением, используя метод Лагранжа.
φ(d1,…, dn) = df + λ (∑di2 – 1). В таком случае величина df, для которой сумма квадратов всех di = 1, достигает максимума, когда достигает максимума следующая функция:
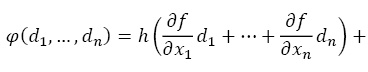
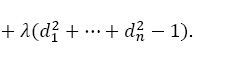
Производная данной функции:
при j = 1,…, n.
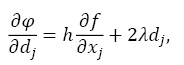
И если 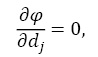 то
то 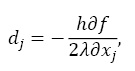
тогда
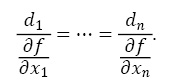
Тогда di ~ ∂f ⁄ (∂xi ,) направление d параллельно 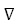 f(x) в точке х.
f(x) в точке х.
Наиболее локальное возрастание функции для заданного малого шага h, имеет место, когда d есть направление 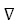 f(x) или g(x).
f(x) или g(x).
В итоге направлением наискорейшего спуска примем –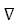 f(x) или –g(x). В простом виде уравнение изменений значений функции можно переписать так:
f(x) или –g(x). В простом виде уравнение изменений значений функции можно переписать так:
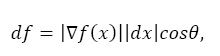
где θ – угол между векторами 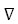 f(x) и dx. Для заданного dx минимизируем θ=1800, и направление dx совпадет с направлением –
f(x) и dx. Для заданного dx минимизируем θ=1800, и направление dx совпадет с направлением –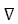 f(x).
f(x).
Направление градиента перпендикулярно в любой точке линии постоянного уровня, поскольку вдоль этой линии функция постоянна. Если (d1 , …, dn ) – малый шаг вдоль линии уровня, то f(x1 + d1, …, xn + dn) = f(x1 , …, xn ).
Следовательно:
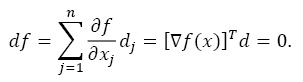
В методе наискорейшего спуска желательно использовать рассмотренное свойство направления градиента, так как на некотором шаге процесса оптимизации поиск минимума функции выполняется вдоль направления – 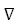 f(xj). Данный метод является итерационным, на шаге I точка минимума аппроксимируется точкой xi.
f(xj). Данный метод является итерационным, на шаге I точка минимума аппроксимируется точкой xi.
Следующей аппроксимацией будет точка:
xi+1 = xi – λi 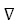 f(xi ), λi – значение λ, минимизирующее функцию
f(xi ), λi – значение λ, минимизирующее функцию
φ(λ) = f(xi – λ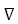 f(xi )).
f(xi )).
Значение λi может быть найдено с помощью методов одномерного поиска. Блок-схема метода может быть представлена следующим образом (рис. 2).
С помощью метода наискорейшего спуска осуществляется поиск из заданной точки в направлении, параллельном одной из осей, до точки минимума в данном направлении. Затем поиск производится в направлении, параллельном другой оси и так далее. На каждом этапе поиск точки минимума производится вдоль «наилучшего» направления. Описанный выше метод позволяет выбрать «наилучшее» направление для оптимизации пьезоэлектрического актюатора по многим критериям.
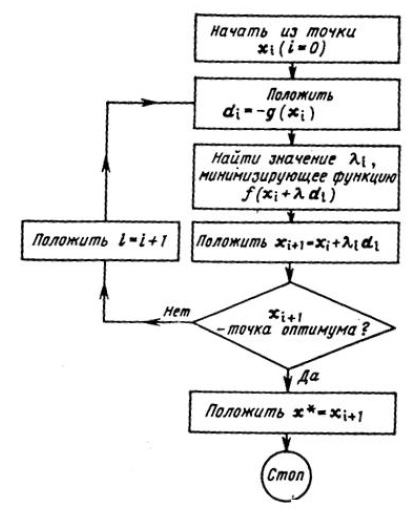
Рис. 2. Схема нахождения значения λi.



