Вязкость (внутреннее трение) – одно из явлений переноса, свойство текучих тел ( жидкостей и газов ) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение. Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей – это описывается введением силы трения.
Различают динамическую (абсолютную) и кинематическую вязкость. В данной работе будет рассмотрена динамическая вязкость. Как известно, динамическая вязкость (μ) – это сила, действующая на единичную площадь плоской поверхности. Эта площадь, по определению, перемещается с единичной скоростью относительно другой плоскости поверхности, находящейся от первой на единичном расстоянии. Поэтому, в системе СИ динамическая вязкость выражается в Па∙с (паскаль-секунда).
Влияние температуры на вязкость жидкостей и газов изучено достаточно хорошо. В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры). Для определения вязкости идеального газа при заданной температуре T (в Кельвинах) может быть использована формула Сазерленда:
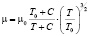 ,
,
где μ0 – контрольная вязкость при некоторой контрольной температуре T0, C – постоянная Сазерленда для того газа, вязкость которого требуется определить. В частности, для азота С = 111К, T0 = 300,55К, μ0 = 17,81 мкПа∙с.
Влияние давления на вязкость имеет большое практическое значение. Однако вследствие значительных методических трудностей, этот вопрос менее изучен, чем зависимость вязкости от температуры.
В ходе проведения эксперимента были получены данные вязкости азота при изменении давления от 3,5 МПа до 68,15 МПа. Температура поддерживалась на уровне 25 °С.
|
Р, МПа |
3,50 |
6,90 |
13,71 |
34,12 |
68,15 |
|
μ, мПа∙с |
0,0185 |
0,0190 |
0,0208 |
0,0286 |
0,0415 |
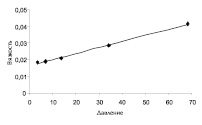
Использование этих данных в качестве координат для изображения соответствующих точек на плоскости Р – μ позволяет сделать вывод о том, что упомянутая зависимость в рассматриваемом интервале давлений близка к линейной μ=b0+b1P .
Для определения коэффициентов b0 и b1 воспользуемся методом наименьших квадратов. Составим сумму квадратов отклонений значений, вычисленных по предполагаемому уравнению, от опытных данных и найдем ее минимум:
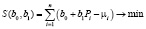 .
.
Поставленная задача приводит к необходимости решения системы уравнений:
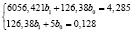 .
.
Решая систему, получим b0=0,0165 и b1=0,00036. Следовательно, искомая зависимость имеет вид: μ=0,0165+0,00036P. Отметим на плоскости Р – μ точки, соответствующие экспериментальным данным, и построим график найденной зависимости. Анализ рисунка подтверждает, что составленная модель хорошо воспроизводит опытные данные. Полученная зависимость позволяет находить приближенные значение вязкостя азота для любого промежуточного давления в рассмотренном интервале.