Молекулярно-кинетическая теория позволяет не только понять, почему вещество может находиться в газообразном, жидком или твердом состояниях, но и объяснить процесс перехода вещества из одного состояния в другое. Фазой вещества называется термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. В однокомпонентной системе разные фазы могут быть представлены различными агрегатными состояниями или разными полиморфными модификациями вещества. В многокомпонентной системе фазы могут иметь различный состав и структуру. Переходы вещества из одного агрегатного состояния в другое, сопровождающееся изменением характера упаковки частиц системы, называются фазовыми переходами первого рода.
Из уравнения Ван-дер-Ваальса в применении к реальным газам следует, что при известных значениях температуры, давления и величин а и b газ образует систему из жидкости и газа (пара). До сих пор нет законченной теории жидкости, и потому мы рассмотрим систему жидкость – пар только с точки зрения учения о физическом равновесии.
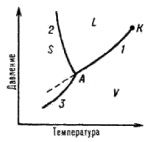
Рис. 1. Диаграмма состояния однокомпонентной системы
Двухфазное равновесие между жидкостью и паром изображается кривой кипения (или испарения) 1, между жидкостью и кристаллами – кривой плавления 2, между кристаллами и паром – кривой возгонки (или сублимации) 3. Здесь S, L и V – соответственно области существования твердой, жидкой и паровой фаз; К – критическая точка; А – тройная точка. Все двухфазные равновесия моновариантны, т.е. не нарушаются при произвольном изменении только одного из параметров, Т или р.
На практике при изучении равновесного состояния жидкость-пар на примере системы: уксусная кислота–диацетат–α–пропиленгликоль были получены следующие данные:
|
x |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|
y |
0,572 |
0,748 |
0,836 |
0,888 |
0,923 |
0,947 |
0,967 |
0,980 |
При введении замены переменных Y=x/y точки с координатами (x;Y) располагаются вдоль некоторой прямой. Рассмотрим линейную зависимость
Y=a+bx => x/y=a+bx => Y=x/(a+bx).
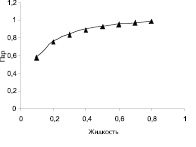
Рис. 2. Диаграмма рассеяния и выравнивающая опытные данные линия регрессии
По формулам парной линейной регрессии вычислим коэффициенты а и b:
b=Sxy/Sx2= 0,915297; a= ȳ – b ∙ x̄ = 0,083993.
Запишем уравнение линейной регрессии: Y=0,915297x+0,083993. Тогда искомая модель примет вид: y=x/(0,915297+0,083993x).
На рис. 2 построен график полученной регрессионной модели. Построенная модель отражает вид функциональной зависимости равновесного состояния жидкость-пар системы уксусная кислота–диацетат–α–пропиленгликоль.



