В различных отраслях промышленности необходимым является получение газа с высоким давлением. В горнодобывающей промышленности применяется воздух с давлением от 0,9 МПа до 70–80 МПа. В первом случае давление необходимо для пневматического привода различного горношахтного оборудования (бурильные установки, отбойные молотки и т. д.), во втором – высокое давление необходимо для воздушных взрывных патронов. В химической промышленности для синтеза, например, аммиака требуется сжатие газа до 32–70 МПа, а при производстве полиэтилена – до 350 МПа (≈3500 атм). Сжатие газа до таких значений давления в одной ступени практически невозможно. Выходом из положения является применение в компрессорах многоступенчатого сжатия с использованием промежуточного охлаждения газа между ступенями сжатия компрессора или просто ступенями компрессора. Для воздушных компрессоров общего назначения чаще всего применяется двухступенчатое сжатие, которое можно рассматривать как частный случай многоступенчатого сжатия.
Рассмотрим двухступенчатое обратимое адиабатическое сжатие газа от начального давления Р1 до конечного Р3. Нахождение оптимальных условий работы будет заключаться в определении промежуточного давления Р2, для которого общий расход энергии является минимальным. При двухступенчатом сжатии работа задается формулой
.
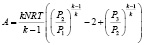где А – работа, кГм; N – количество сжимаемого газа, кг-мол; R – газовая постоянная; k – отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме (показатель адиабаты); Т – температура поступающего в компрессор газа.
Найдем производную составленной функции по переменной P2 и приравняем полученную производную к нулю
.
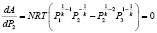Решая уравнение относительно переменной P2, найдем значение для промежуточного давления при двухступенчатом сжатии газа: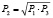 
.
Для того, чтобы убедиться, что найденное значение P2 соответствует минимальному значению работы, вычислим вторую производную от функции А:
.
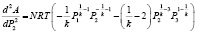Подставляя выражение для Р2, получим
.
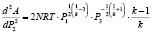Так как для любого газа показатель адиабаты превышает единицу, то вторая производная функции А в рассматриваемой точке положительна. Следовательно, при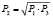 
функция работы достигает своего минимального значения.
В полученном выражении для Р2 отсутствует величина k, следовательно, оно справедливо для любого политропического сжатия.
Решенная нами задача о компрессоре может быть обобщена на случай трехступенчатого сжатия.