В настоящее время существует множество программных комплексов позволяющих решать задачи компьютерного моделирования с применением высокопроизводительных вычислений. Большинство таких комплексов решают задачи по моделированию систем относящихся либо к классу с дальнодействующими потенциалами, либо учитывающими только короткодействующие ковалентные взаимодействия [1-3].
Принципиальное отличие систем, являющихся предметом исследования данной работы, состоит в том, что это полимеризующиеся системы с многочастичным взаимодействием, объединяющим несколько видов взаимодействий: двухчастичные вклады (дальнодействующие ионные и близкодействующие отталкивательные) и многочастичные (двух и трех-частичные ковалентные взаимодействия)[6-8]. Моделирование полимеризующихся систем является нетривиальной задачей, требующей учета особенностей ионного и ионно-ковалентного взаимодействия частиц разных типов в расплаве. Это существенным образом усложняет постановку задачи распределения.
На основе концептуальной модели и тщательного анализа программного кода локального МД-приложения [6], автором разработана модель неоднородных дескрипторов, обеспечивающая возможность распределения и распараллеливания расчетов для коррелированных многочастичных систем, на основе «свертки» детализации физического описания объектов [5].
Предметом данной работы является разработка метода позволяющего применять вычислители на основе графических процессоров для расчетов системы N-частиц, что даст возможность распределить расчет дескрипторов между миллионами нитей и серьезно сократить время КМ. На рисунке представлен алгоритм расчета дескрипторов с использованием центрального и графического процессора.
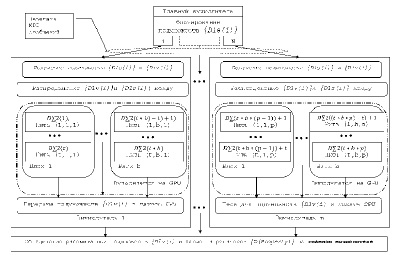
Алгоритм расчета дескрипторов с использованием центрального и графического процессора
Передача подмножеств дескрипторов каждому вычислителю производится с использованием технологии MPI, а параллельный расчет реализуется на графических процессорах с применением технологии CUDA.
На главном вычислители формируются подмножества дескрипторов {Dls(i)}, {Dlv(i)} c мощностью k=N/p, где N – количество дескрипторов, p – количество вычислителей выполняющих расчет. Сформированные подмножества передаются вычислителям через интерфейс передачи сообщений MPI. Полученные подмножества дескрипторов распределяются центральным процессором между нитями, реализующими расчет на графическом процессоре, где индекс t – количество нитей в блоке, b – количество блоков. На каждой нити графического процессора, с использованием технологии CUDA, рассчитываются значения элементов одного двухчастичного агрегатора D∑2(i). На основе результатов расчета подмножест двухчастичных агрегаторов обновляются значения элементов дескрипторов {Dlv(i)}. Полученные подмножества дескрипторов {Dlv(i)} передаются на центральный процессор. После завершения расчетов всеми вычислителями рассчитанные подмножества одночастичных векторных дескрипторов объединяются на главном вычислителе для расчета агрегатора {D(Property)}.
Проведенные компьютерные эксперименты, результаты которых представлены в таблице показывают существенное сокращения времени проведения КМ за счет совместного использования технологий CUDA и MPI.
Результаты моделирования системы SiO2 (в часах)
|
N |
Локальный вариант |
MPI-8 |
MPI-16 |
CUDA |
CUDA-2 |
|
1000 |
3,1 |
0,41 |
0,22 |
0,17 |
0,09 |
|
4200 |
11,5 |
1,75 |
0,9 |
0,63 |
0,37 |
|
12000 |
134 |
21,7 |
10,3 |
7,4 |
4,1 |
|
100000 |
1456 |
221 |
87,6 |
77,3 |
39,3 |
В моделирование сравнивалось время, затраченное на проведение эксперимента с числом частиц в системе 105 и числом шагов 5000.
Компьютерные эксперименты проводились на кластере, состоящем из 16 вычислителей Dual Core AMD Opteron с частотой 2.21 Ghz для приложения, реализованного с использованием технологии MPI. На графическом процессоре с использованием двух видеокарт NVidia GeForce GTS 450 для приложения реализующего расчет на CUDA.
Полученные результаты дают возможность говорить о целесообразности использования графических процессоров для экспериментов в области молекулярной динамики и позволяют ускорять время расчета в 36 раз по сравнению с локальным вариантом МД-приложения.



