Для решения прямой задачи линейного программирования, можно воспользоваться решением двойственной задачи. Под двойственной задачей понимается вспомогательная задача линейного программирования, формулируемая с помощью определённых правил непосредственно из условий прямой задачи. Интерес в определении оптимального решения прямой задачи с помощью решения двойственной к ней задачи вызван тем, что вычисления при решении двойственной задачи менее сложные. Прибегая к такому решению, покупатель может найти такой набор цен ресурсов, имеющихся у производителей, при котором затраты на приобретение этих ресурсов будут минимальны, а производитель получит при этом прибыль не менее той, какую бы он получил при производстве и сбыте готовой продукции. Рассмотрим на примере.

Нам дана функция: L= –2X1+4X2+14X3+2X4 min

при этом ограничения:

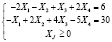
Решим исходную задачу, решая двойственную. Учтем несимметричный характер пары двойственных задач (II тип).

Введем матрицы

, ,

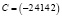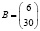Тогда двойственная задача примет вид:

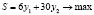
Система ограничений:

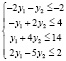
Тогда график функции будет выглядеть так:

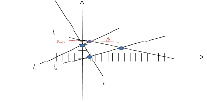
Область допустимых решений – ABCD.

Мы получаем следующий вывод: максимальное значение S равно 102, при этом максимальный план равен Y=.

Вернемся к исходной задаче.

Теперь система ограничений исходной задачи примет вид:

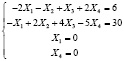
В итоге мы получаем: минимальное значение L равно 102, при этом минимальный план равен

.

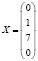Теория линейного программирования позволяет не только получать оптимальные планы с пoмощью эффективных вычислительных процедур, нo и делать ряд экономически содержательных выводов, основанных на свойствах задачи, которая является двойственной по отношению к исходной ЗЛП.