Решим задачу о распределении 100 предприятий по сумме отчислений в пенсионный фонд X (тыс.руб) и на социальное страхование работников Y (тыс.руб.) (таблица).
Вычислим первоначальные данные для корреляционной зависимости.
Общие средние.
Среднее арифметическое всех значений CВ X: 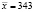
Среднее арифметическое всех значений CВ Y: 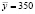
|
Y X |
100-200 |
200-300 |
300-400 |
400-500 |
500-600 |
Итого |
_ yx |
|
|
150 |
250 |
350 |
450 |
550 |
||||
|
50-150 |
100 |
5 |
3 |
- |
- |
- |
8 |
187,5 |
|
150-250 |
200 |
7 |
8 |
- |
- |
- |
15 |
203,3 |
|
250-350 |
300 |
- |
8 |
13 |
5 |
- |
26 |
338,5 |
|
350-450 |
400 |
- |
4 |
10 |
8 |
6 |
28 |
407,1 |
|
450-550 |
500 |
- |
- |
9 |
6 |
8 |
23 |
445,7 |
|
Итого: |
12 |
23 |
32 |
19 |
14 |
100 |
||
|
_ xy |
158,3 |
256,5 |
387,5 |
405,3 |
457,1 |
|||
Общее среднее квадратическое отклонение:
σx = 121,86 σy = 120,83.
Межгрупповое среднее:
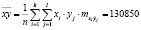 .
.
Межгрупповая дисперсия:
δ²ₓ =9008,37 δ²y =8394,39.
Вычисленные корреляционные отношения: ηyx =0,758 ηxy =0,779 показывают, что между случайными величинами X и Y имеется сильная (тесная) корреляционная зависимость.
Коэффициент корреляции
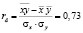 .
.
подтверждает сильную возрастающую линейную зависимость.
Составим по вычисленным данным уравнения линейной регрессии.
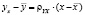 ,
,
где ρyx = 0,72; yx=0,72x+103,04.
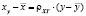 ,
,
где ρxy =0,74; xy=0,74y+84.
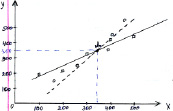
Рис. 1
– – – – прямая xy=0,74y+84;
___ – прямая yx=0,72x+103,04;
– условные средние yx;
– условные средние xy;
• – M0(x, y) – точка пересечения прямых регрессии, где x=343 y=350
Средние квадратические ошибки: Sξy=31,65 Sξx=39,87
Поскольку Sξy < σy и Sξx < σy, то найденные модели линейной регрессии целесообразно использовать в расчетах.



