Запасы создаются на любом предприятии и зачастую причинами их создания являются различия в темпах производства и потребительского спроса. Под запасами можно понимать такое количество материалов, ресурсов, с помощью которого ведется непрерывно выпуск товаров. Ими же могут являться и сезонные товары, находящиеся в резерве выпускаемой продукции. Следовательно, сезонность является одной из важнейших причин создания запасов. На наш взгляд важно также отметить тот факт, что создание запасов является очень затратным процессом – их необходимо где-то хранить. К тому же, в процессе хранения, большинство запасов теряет свои характеристики и морально устаревают. Соответственно возникают разного рода проблемы в управлении этими запасами [1].
Сущность управления запасами заключается в установлении баланса между объемами заказа и вновь прибывшей партии товара.
Для более эффективного управления, использования создаются различные методы, модели теории управления запасами. Системы управления запасами можно классифицировать по различным признакам: по месту хранения, по виду запасов, по их свойствам, информационным характеристикам и так далее. В связи с этим очень сложно построить такую модель, которая удовлетворяла бы все условия запасов [2].
Оптимальное управление запасами достигается за счет правильного выбора объема и времени поставки. Это достигается тогда, когда суммарные издержки производства являются минимальными.
В данной статье мы рассмотрим несколько моделей управления запасами.
Самой распространенной и наиболее часто применяемой, является модель оптимального размера заказа. В данной модели спрос (D) в рассматриваемый период времени постоянен, как и цена приобретения (P), а расходы на хранение (H) здесь определяются как постоянная сумма издержек на единицу товара:
,
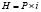где i – коэффициент затрат на хранение запасов.
Оптимальный размер заказа рассчитывается по следующей формуле:
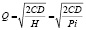
C – затраты на размещение одного заказа; Q – размер заказа; L – цикл заказа;
Точка заказа (PL) будет равна:
.
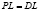А время (t) между заказами:
.
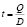Учитывая тот факт, что спрос и цена в данной модели постоянны, то важно отметить то, то ч точки зрения оптимизации суммарных затрат на управление запасами они не представляют абсолютно никакого интереса. В данной модели имеет место оценка затрат на оформление заказа и затрат на хранение (z):
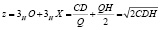[4].
Рассмотрим данную модель, для более точного понимания, на примере.
Оптовый продавец имеет спрос на 300 единиц товара X в месяц. Затраты на приобретение единицы товара со стороны покупателей составляет 80 рублей. Затраты на хранение единицы товара со стороны оптовика равны 15 % от его среднегодовой стоимости. Стоимость оформления одного заказа составляет 150 рублей, независимо от количества. Необходимо рассчитать оптимальный размер заказа и все значимые затраты.
Итак, необходимо ввести обозначения:
C = 150
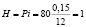
D = 300.
Из данных следует, что
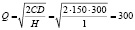единиц ресурса.
Рассчитывая суммарные затраты на оформление и хранение, мы воспользуемся формулой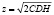 
.
А периодичность будет равна: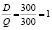 
, т.е 1 заказ в месяц.
При применении такой модели, а так же других, важно учитывать следующие факторы:
• спрос очень часто имеет значительные колебания, следовательно – являются серьезной сезонной составляющей;
• очень часто контроль использования и надлежащего качества запасов затруднен на практике;
• цикл не обязательно должен быть детерминированным.
Существуют так же и другие модели управления запасами. Например, обобщенная модель управления запасами. В данной модели управление запасами исходит из характера спроса. В этом случае спрос может быть достоверно известным (детерминированным) и задаваемым плотностью вероятности, т.е. вероятностным. Так же в свою очередь каждый из этих видов спроса делиться на составляющие:
Детерминированный спрос:
• Статический;
• Динамический.
Вероятностный спрос:
• Стационарный;
• Нестационарный.
Данная классификация можно сказать отображает уровни обобщения спроса:
В течение всех периодов, в которых ведутся исследования спроса, используется одна и та же функция распределения вероятностей. В данном случае все значимые колебания спроса не учитываются в модели.
Учитывается изменение спроса от одного периода к другому. Однако при этом в каждом периоде функции распределения не применяются. На этом уровне сезонные колебания учитываются.
Элементы риска и изменения спроса исключаются. И таким образом, спрос в течение любого периода рассматривается как равный среднему значению известного спроса.
Следующая модель, на которой мы хотели бы акцентировать внимание, называется модель размера производственного заказа. В этой модели, для более полного понимания, в качестве запаса предлагается рассмотреть комплектующие для сборки. В этом случае держатель запасов может одновременно являться и их поставщиком. Следовательно, уровень запасов растет постепенно. Важно также отметить, что данная модель используется в том случае, если норма выработки ресурса превышает спрос за аналогичный период (R>D), где R – норма выработки за период времени, а D – спрос.
Следовательно, оптимальный размер производственного заказа (Q), рассчитывается:
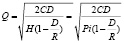
C – затраты на накладку производства; H – затраты на хранение единицы запаса; I – коэффициент затратности на хранение.
Время между началами двух циклов производства (T) рассчитывается:
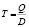
и, следовательно, время производства (t) будет равным:
.
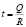Точка заказа (PL) здесь зависит от величины цикла (L) заказа и времени застоя производства:
,
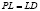при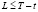 
[4].
Подводя итоги данной статьи, мы отмечаем, что рассмотрели не все модели управления запасами, а только лишь часть из них. Любая из моделей помогает просмотреть изнутри всякого рода проблемы и возможные их решения. Хотя, в большинстве случаев это является лишь первым шагом на пути решения проблемы. Известные нам модели управления запасами, довольно-таки редко абсолютно точно описывают реальную систему. Следовательно, решение, получаемое на основе моделей этого класса, следует рассматривать только лишь как выводы. [3]