N-мерный вектор и векторное пространство являются предметом изучения линейной алгебры и представляют немалый интерес в науке и исследованиях. Так как они носят не только теоретический характер, но и имеют вполне реальное практическое применение в современном мире. Ведь знание фундаментальных основ линейной алгебры, а в частности ее раздела аналитической геометрии способствует формированию специализированных знаний, представляющий собой синтез профессиональных навыков и умений узких специалистов, и широких общенаучных фундаментальных знаний.
И если раньше научный интерес вызывал исключительно геометрический анализ экономических задач, то в наши дни объединение таких наук как физика и информатика с данным разделом высшей математики, является весьма прогрессивным направлением.
Особенно в связи с появлением все большего количества портативных гаджетов на операционных мобильных системах, таких как всем известные титаны Android и IOS, BlackBerry OS Windows Mobile не пользующиеся такой же огромной популярностью, а так же мало известные новички рынка операционных систем Tizen, Sailfish,Firefox OS, Ubuntu Mobile.
Мы тесно контактируем с этим разделом векторной алгебры, сами того не замечая, а ведь все мобильные приложения на наших телефонах, в которых применяется позиционирование экранных кнопок, работа с камерой и ее направлением, изменение скоростей объектов и.т.д., основаны на свойствах n-мерных векторов, векторных пространств и действиями над ними.
Именно поэтому, выбранная нами, тема является весьма актуальной на сегодняшний момент. Для детального изучения данной темы введем основные понятия, изучаемые в разделе векторной алгебры.
N-мерным вектором называется упорядоченная совокупность n действительных чисел, записанных в виде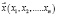 
, где x – называется компонентами вектора или координатами вектора.
Рассмотрим основные свойства n-мерного вектора:
1. 
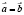, если их координаты равны, т.е.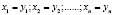 
2. 
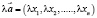
3. 
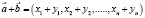
И свойства операций над ним:
1. 
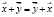– переместительный закон
2. 
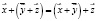– сочетательный закон
3. 
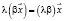– сочетательный закон относительно скалярного произведения
4. 
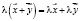
5. 
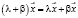
6. Для всякого вектора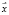 
есть противоположный ему 
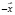, такой, что сумма этих двух векторов равна нулю: 
.
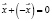7. Существует вектор ноль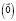 
такой, что 
; 
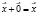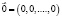
8. Если умножить 1 на вектор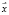 
, то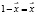 
Именно из этих свойств над операциями вытекает следующее определение.
Множество векторов с действительными компонентами, в котором определены операции сложения и умножения вектора на число и удовлетворяющее приведенным выше 8 свойствам, рассматриваемым как аксиома – называются векторным пространством.
Ярким примером практического использования n – мерного вектора и векторных пространств в компьютерной графике является процесс твининга и экстраполяции.
Твиниг – это особый вид анимации, показывающий постепенные превращения одной фигуры в другую, В основном он используется в киноиндустрии для уменьшения стоимости создания мультипликационных фильмов.
Если раньше художнику было необходимо рисовать все 24 кадра, то в наши дни он может самостоятельно создать только ключевые кадры в определенной последовательности, а остальное предоставить компьютеру, который сам способен воссоздать недостающие элементы при помощи экстраполяции и воссоздать иллюзию движения или перемещения при помощи твининга.
В основном эти методы использовались в двумерных пространствах и базировались на операциях с обычными векторами, но с развитием 3D технологий все чаще и чаще применяются n-мерные вектора и, соответственно, векторные пространства, образованные ими.
Основная формула данных преобразований имеет вид: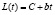 
, где: L – траектория перемещения, изменения или движения изображения; t – положение точки на прямой, относительно которой происходят перемещения; C и b – n-мерные векторы (в основном используются 3-х и 4-х мерные). Расчет происходит на основании приведенных выше свойств и операций. В зависимости от конкретной ситуации и сложившейся сложности, данная формула может видоизменяться.
В ходе работы над данной статьей мы дали определение n-мерного вектора, рассмотрели операции над n-мерными векторами, их свойства и увидели, что множество всех n-мерных векторов с определенными на нем операциями сложения и умножения на число порождают векторное пространство.
Основываясь на данной теоретической базе, мы также рассмотрели данные элементы линейной алгебры в области компьютерной графики. Что является весьма актуальным в наш век передовых технологий и постоянно развивающихся ЭВМ. Также этому способствовало развитие трехмерного изображения, которое используется повсеместно.
Проделанная работа показывает, насколько близко мы контактируем с данным разделом линейной алгебры, даже не задумываясь об этом. Ведь практически любой из нас пользуется мобильными приложениями, играет в компьютерные игры, смотрит мультипликационные фильмы, но мало кто задумывался о том при помощи чего это создано все то, с чем мы сталкиваемся настолько часто.
Именно это и доказывает актуальность и важность, выбранной нами, темы, которая, несомненно, достойна подробного изучения и пристального внимания к ней.