Согласно проведенным исследованиям одной из весьма распространенных форм представления математических моделей являются так называемые передаточные функции для скалярной системы и матричные передаточные функции для матричной системы. Эти функции представляют собой записанную в явном операторном виде непосредственную связь сигналов на выходе системы с входными воздействиями.
Возьмем за основу операторное уравнение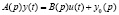 
. Принципиально то, что матрица A(p) всегда является квадратной и в общем случае имеет вид
.
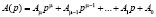Или
.
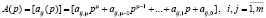Матрица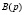 
имеет аналогичный вид с учетом ее размера 
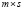. Здесь m – старшая степень полинома, часто называемая порядком полинома; i, j – номера соответственно строки и столбца, которым принадлежит записанный элемент матрицы. Будем полагать, что 
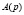и 
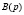– взаимно просты слева, если они не имеют общих левых делителей, отличных от единичной (точнее, унимодулярной)[1] матрицы.
В случае скалярных систем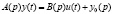 
представляет собой скалярное уравнение. Матрицы 
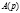и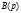 
вырождаются в скалярные полиномы a(p) и b(p). Переход от этой записи к записи
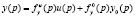
осуществляется формально делением всего уравнения на полином a(p).
Конструкция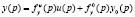 
в теории автоматического регулирования получила название оператора системы, включающего две дроби
;
.
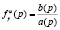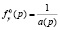Первая из этих дробей представляет собой передаточную функцию системы от входного воздействия u к выходной величине y (или передаточную функцию по входному воздействию). Эта функция определяет составляющую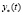 
. Вторая дробь представляет собой передаточную функцию от начальных условий системы, выраженных оператором 
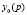, к выходной величине y (или передаточную функцию по начальным условиям). Эта функция определяет составляющую свободного или собственного движения системы.
Значения корней уравнени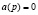й 
и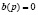 
на комплексной плоскости 
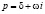получили названия полюсов 
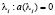и нулей 
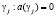передаточной функции 
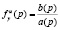соответственно. При объединении полюсов передаточной функции 
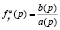, используют обозначение 
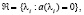а нулей – 
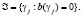Множество корней характеристического уравнения 
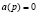скалярной системы называется спектром передаточной функции или спектром системы.
Заметим, что полюсы и нули содержат всю информацию о динамических свойствах скалярной линейной системы. Так, полюсы, полностью определяя передаточную функцию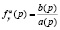 
, отражают характер внутренних связей в системе. Они показывают, как система ведет себя «вне связи» с внешним миром. При исследовании только собственных или свободных движений системы достаточно анализировать размещение полюсов на комплексной плоскости (модальный анализ). Нули же (наряду с полюсами) отражают свойства передаточной функции 
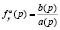и показывают характер связей системы с ее окружением, т.е. с внешними воздействиями, поступающими на вход.
Теперь перейдем к системам, имеющим несколько (s) входов и несколько (m) выходов. В случае, когда степень характеристического полинома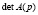 
равна порядку n, система 
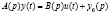считается нормализуемой, поскольку ее можно разрешить относительно высших производных. Действительно, путем обращения матрицы A(p) из уравнения 
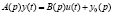может быть получена конструкция
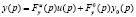
где введены следующие дробно-рациональные полиномиальные матрицы:
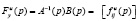
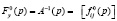
с аналогичным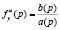 
смыслом.
В подавляющем большинстве работ по матричным (многосвязным) системам исследуется только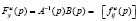 
. Матрица 
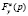размера 
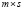представляет собой совокупность 
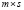скалярных передаточных функций 
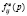. Каждая такая функция является скалярной передаточной функцией от j-го входа к i-му выходу. Такая матрица формализует интуитивное представление об обобщении скалярного случая на многомерный .
В общем случае матричные передаточные функции имеют алгебраическую особенность в виде некоммутативности, т.е. они не допускают изменения порядка следования при умножении. Последовательное соединение двух матричных систем соответствует записи
.
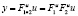Сигнал здесь вначале проходит систему с матрицей передаточных функций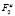 
, а затем 
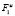. Каждый элемент обобщенной матрицы 
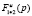передаточных функций определяется формулой, которую, не принимая во внимание сократимость полиномиальных дробей, можно записать в виде
.
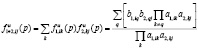где в числителе фигурирует суммирование полиномов. Собственные значения полиномиальных уравнений
.
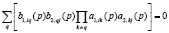для каждой новой скалярной передаточной функции определяются непосредственным вычислением. Множество полюсов для скалярной передаточной функции образуется объединением множеств полюсов j-го столбца первой системы и i-ой строки второй системы по ходу сигналов.
Формула
,
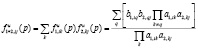а точнее возникновение сложности в вычислении нулей (именно нулей), показывает, что переход от скалярных систем к матричным системам путем, как часто говорили, простого обобщения, не имеет под собой формальных оснований. Матричные системы представляют собой качественно новые объекты теории систем.
[1] Обратимой матрицы с единичным детерминантом.