При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции получать новую функцию, которую называют производной функцией (или просто производной) данной функции, процесс получения новой функции был назван дифференцированием.
Использование производной применяется во многих науках, но в данной статье хотелось бы осветить использование производной в сфере экономики.
В экономической теории активно используется понятие «маржинальный» или «предельный». Следует отметить, что маржинализм – направление, возникшее в XIX веке в экономической науке, признающее высокую роль предельных (маржинальных) величин в науке, речь о которых пойдёт далее.
Важный раздел методов дифференциального исчисления, используемых в экономике – методы предельного анализа, то есть совокупность приемов исследования изменяющихся величин затрат или результатов при изменениях объемов производства, потребления и т. п. на основе анализа их предельных значений.
Теоретический анализ разнообразных явлений экономики использует ряд предельных величин. Перечислим лишь некоторые из них: предельная стоимость, предельные издержки, предельный доход, предельная производительность, предельная полезность, предельная склонность к потреблению. Все эти величины самым тесным образом связаны с понятием производной.
Таким образом, предельный показатель (показатели) функции – это ее производная. Как говорилось выше, в экономике часто используются средние величины, но требуется узнать, на какую величину вырастет результат, если будут увеличены затраты или наоборот, насколько уменьшится результат, если затраты сократятся. С помощью средних величин ответ на этот вопрос получить невозможно. В подобных задачах требуется определить предел отношения приростов результата и затрат, то есть найти предельный эффект.
Следовательно, для их решения необходимо применение методов дифференциального исчисления.
В качестве характерного примера рассмотрим предельные издержки. Следует заметить, что предельные издержки – это затраты, связанные с выпуском одной дополнительной единицы продукции. Пусть y(x) затраты на изготовление х экземпляров некоторого продукта. Тогда y'(x) выражает скорость изменения затрат при изменении количества продукта. Эта производная называется предельной (маржинальной) стоимостью.
Согласно определению производной имеем:
.
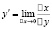Следовательно, можно считать, что производная y'(x) приближенно равна отношению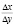 
. Пусть ∆x=1. На практике обычно х – очень большое число, так что единица мала по сравнению с х. Откуда:
.
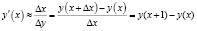Разность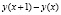 
выражает на сколько изменились затраты (издержки) при изготовлении ещё одного экземпляра продукции, поэтому экономисты определяют предельные издержки y'(x) так же, как и затраты на изготовление одного экземпляра продукции.
Приведём пример. Пусть зависимость между издержками продукции «у» и объемом выпускаемой продукции «х» на предприятии выражается функцией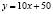 
. Определим предельные издержки при объеме продукции x=100 единиц.
Поскольку предельные издержки выражаются производно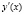й 
, при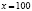 
предельные издержки составят y'(100)=10. Это означает, что при данном уровне производства (количестве выпущенной продукции 100 единиц) на выпуск единицы дополнительной продукции необходимы дополнительные затраты в 10 денежных единиц. Действительно, затраты на выпуск сто первой единицы продукции можно подсчитать и по другому:
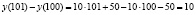
Для нашего примера (в случае, когда «у» является линейной функцией от переменной х) разность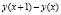 
совпадает со значением производной 
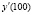. В общем же случае (когда функция y(x) может быть нелинейной) при больших «х» разность 
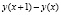совпадает с y'(x) лишь приближенно.
Как видно, предельная величина характеризует не состояние (как суммарная или средняя величина), а процесс (как изменение экономического объекта). Таким образом, предельная величина выступает как скорость изменения некоторого экономического объекта (процесса).
Помимо предельных издержек с помощью производной могут быть определены: предельных доход, предельная стоимость, предельный спрос, предельная выручка, предельная производительность труда и другие предельные величины.
Понятно, что использование этих методов имеет немаловажную роль в решении экономических задач различного характера.
Определение предельных величин с помощью понятия производной позволяет использовать математический аппарат для доказательства экономических законов.
Приведём яркий пример применения дифференциального исчисления в экономической теории.
Пусть «х» – количество реализованного товара, R(х) – функция дохода, С(х) – функция издержек (затрат на производство товара). Вид этих функций зависит от способа производства, оптимизации, инфраструктуры и т.п. Обозначим функцию прибыли как P(x). Тогда:
.
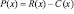Очевидно, оптимальным уровнем производства является тот, при котором прибыль максимальна, то есть такое значение выпуска «х», при котором функция Р(х) имеет максимум. Следовательно, в этой точке:
.
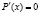Но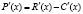 
. Поэтому 
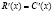, то есть если уровень выпуска продукции «х» является оптимальным для производителя, то:
,
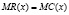где MR(x) – предельный доход; MC(x) – предельные издержки.
Благодаря применению производных, мы получили известное в экономической науке утверждение «Для того, чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны», – что подтверждает, важность использования математического аппарата для доказательства экономических законов.
Таким образом, применение математических методов в экономике не ограничивается применением производных, осуществленным в идеях маржиналистов, а очень широко распространено и постоянно развивается и совершенствуется.