Движение жидкостей представляет собой сложное физическое явление, зависящее от многих факторов всегда связанных друг с другом, причем связь между ними выражает физический закон, характеризующий данное явление. Плодотворным методом исследования является применение теории подобия – учение о методах научного обобщения эксперимента. Применение данной теории позволяет выполнять необходимые исследования на моделях небольшого размера, а не на промышленной дорогостоящей аппаратуре. Кроме того, опыты можно проводить не с агрессивными, опасными веществами, а с модельными (водой).
Движение жидкости в трубопроводе характеризуется не только распределением скоростей, но и другими факторами: вязкостью жидкости, ее плотностью и др. Основываясь на теории подобия, для того чтобы жидкость в двух разных трубопроводах двигалась подобно, в их сходственных точках должны быть равны некоторые безразмерные соотношения физических величин, влияющих на движение жидкости. Эти безразмерные соотношения разнородных физических величин называются критериями подобия.
Основными критериями подобия гидромеханических процессов являются:
Кинематический критерий (критерий Рейнольдса), характеризующий действие сил трения в подобных потоках и определяющий режим движения жидкости: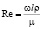 
, где ω [м/c] – скорость движения жидкости, l [м] – определяющий размер, r [кг/м3] – плотность жидкости, m [Па·с] – коэффициент кинематической жидкости.
Гравитационный критерий (критерий Фруда), характеризующий действие сил тяжести в подобных потоках: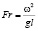 
, где g[м/c2] – ускорение свободного падения.
Критерий гидравлического сопротивления (критерий Эйлера), характеризующий действие сил давления в подобных потоках: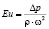 
, где ∆p[Па] – потери давления.
При моделировании исходят из равенства только тех критериев, которые отражают влияние сил, имеющих наибольшее значение для данных условий.
Решим практическую задачу с использованием теорем подобия: Какой должен быть взят геометрический масштаб модели, если в промышленном аппарате рабочая жидкость – нефть, а в модели – вода, кинематический коэффициент вязкости в 50 раз меньше, чем у нефти? Какую скорость надо дать воде в модели, если скорость нефти в промышленном аппарате 1 м/с? Моделируются одновременно силы трения и силы тяжести.
Решение. Согласно первой теореме подобия: подобные явления характеризуются равными критериями подобия (выведена Ньютоном). По условию моделируются силы трения и силы тяжести. Значит, будем оперировать критерием Рейнольдса (Re) и критерием Фруда (Fr). Обозначим физические параметры нефти индексом «Н», модели воды – «В».
Расчетную формулу для критерия Рейнольдса целесообразнее использовать с коэффициентом кинематической вязкости жидкости «ϑ» – что следует из условия задачи: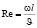 
, где J [м2/c] – коэффициент кинематической вязкости. Получаем: 
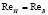, откуда 
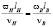. По условию задачи: 
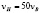. Тогда 
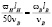или 
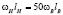. По условию, 
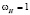м/с, поэтому 
.
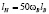Моделируются силы тяжест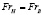и: 
или
,
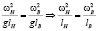но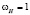 
м/c, поэтому 
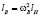или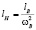 
. Приравниваем: 
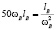. В результате преобразований, получаем: 
.
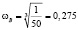Таким образом, скорость воды в модели должна быть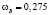 
м/c.
Далее необходимо определить соотношение определяющих размеров натуры (промышленного аппарата) и модели, то есть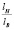 
. Имеем 
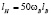или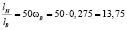 
. Таким образом, 
.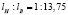