Анализ конечных изменений направлен на решение важной и распространенной на практике задачи поиска величины влияния изменений факторов на изменение определяемого ими результирующего показателя.
Пусть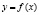 
– некоторая функция, характеризующая поведение результативного показателя или процесса; x1, x2,…, xn – факторы, от которых зависит показатель. Задана функциональная детерминированная форма связи изучаемого показателя (у) с набором факторов x1, x2,…, xn; 
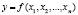. Пусть результативный показатель (у) получил приращение (Δy) за анализируемый период. Требуется определить, какой частью численное приращение функции 
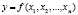обязано приращению каждого аргумента (фактора) Δx=(Δxi) по сравнению с начальным значением. Именно таким образом можно сформулировать основную задачу для рассматриваемого анализа [4].
Для составления рабочих формул необходимо учитывать принцип построения модели и вид, к которому она относится [1, 6, 7].
Аддитивная модель является математическим уравнением, где результативный показатель представлен в виде алгебраической суммы нескольких факторных признаков:
.
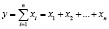Мультипликативная модель отражает прямую пропорциональную зависимость исследуемого обобщающего показателя от факторов:
.
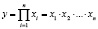Кратная модель результативного показателя у от факторов математически отражается как частное от их деления и имеет следующий вид:
.
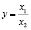Смешанная модель представляет собой сочетание различных комбинаций аддитивной, мультипликативной и кратной зависимостей [6]. Приведем некоторые примеры такой зависимости:
,
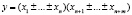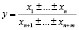или 
.
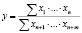Для изучения изменения показателей и степени их влияния используют разные способы, применение которых зависит от цели и глубины анализа, объекта исследования, технических возможностей выполнения расчетов и т.д.
Широкое распространение в аналитических расчетах получил метод цепных подстановок. Он используется для расчета влияния факторов во всех типах моделей, принцип построения которых приведен выше.
Алгоритм расчета анализируемой модели методом цепных подстановок в случае функции нескольких переменных можно представить в следующем виде:
1) Базовое (плановое) значение результирующего показателя:
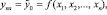где n∈Z+.
2) Промежуточные значения результирующего показателя:
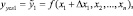
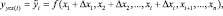где i = 2,…,n-1.
3) Фактическое значение результирующего показателя:
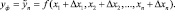
4) Общее абсолютное изменение результирующего показателя:
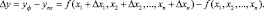
5) Изменение результирующего показателя за счет изменения i-го фактора:
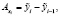где i = 1,…,n.
При этом остается верным соотношение:
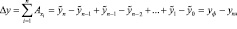. [5]
Метод цепных подстановок позволяет сделать расчет для любой существующей модели, но его недостаток состоит в том, что он не учитывает распределение неразложимого остатка между существующими факторами, а относит его к последнему в порядке изменения показателю. Таким образом, прирост обобщающего показателя за счёт совместного изменения факторов приписывается влиянию только качественного фактора, т.к. по правилу использования данного метода он заменяется в последнюю очередь. Также, существенным недостатком является то, что в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. В то же время, при замене равноценных факторов (например, качественных) зависимость влияния на прирост фактического результирующего значения не наблюдается [2].
Например, рассмотрим двухфакторную мультипликативную модель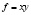 
, факторы x и y которой получают соответственно приращения Δx и Δy. Тогда результирующий показатель изменится на:
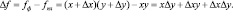
При анализе подобной ситуации можно прийти к тому, что неразложимый остаток ΔxΔy будет отброшен или интерпретирован как логическая ошибка (при достаточно малых значениях приращения факторов в редкой для современной экономики ситуации) [4]. Метод цепных подстановок же приводит к двум различным видам представлений Δf:
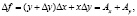
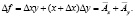
Как показывает практика, обычно применяется второй вариант при условии, что x – количественный фактор, а y – качественный. В этом случае выражение для оценки влияния качественного фактора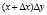 
более активно, поскольку его величина устанавливается умножением приращения качественного фактора на отчётное (фактическое) значение количественного фактора. Тем самым весь прирост обобщающего показателя за счёт совместного изменения факторов (ΔxΔy) приписывается влиянию только качественного фактора [5].
Таким образом, задача точного определения роли каждого фактора в изменении результирующего показателя обычным методом цепных подстановок не решается. Но, существует универсальный метод, позволяющий однозначно оценить величины факторного влияния на результирующий показатель – метод конечных приращений, основанный на применении теоретических сведений классического математического анализа.
Именно теорема Лагранжа о среднем дифференциального исчисления сыграла решающую роль в данном аспекте, поэтому именно она стала основой для разработки универсального метода экономического факторного анализа, применимого в условиях произвольных конечных приращений факторов.
Дифференциальная теорема Лагранжа о среднем значении, записанная для функции нескольких переменных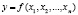 
, позволяет перейти к формуле 
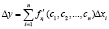. Т.к. 
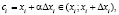где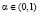 
, то справедлива формула:
,
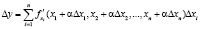где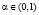 
– параметр, который используется при анализе модели, если существует необходимость более тщательного исследования влияния изменения факторов на вариацию результирующего показателя.
Влияние изменения факторов на изменение результирующего показателя имеет следующую формулу, позволяющую решить основную задачу анализа конечных изменений:
.
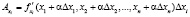При этом,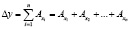 
[5].
Значительное преимущество данного способа заключается в том, что метод конечных приращений (метод Лагранжа) позволяет найти точное значение степени влияния некоторого фактора на изменение результирующего показателя, что, несомненно, даёт не только оптимальный подход к решению, но и подходящий алгоритм для широкого спектра исследований при помощи анализа конечных изменений [3].
Таким образом, можно изобразить различие в расчетах различными методами, представленное на рисунке [2].
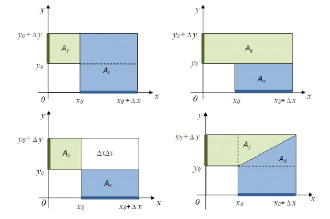
Иллюстрация расчетов различными методами
Для метода конечных приращений характерна высокая точность в расчетах, а также простота составления формул. Таким образом, данный способ разложения функции является наиболее оптимальным по сравнению с методом цепных подстановок.
На практике часто возникает потребность в использовании специализированных методов анализа конечных изменений, которые позволяют учесть дискретную структуру анализируемых факторов, когда оценка влияния на результирующий показатель производится с учетом динамики показателей [5]. В таком случае можно говорить о цепном анализе конечных изменений, который учитывает неоднородность производственных и хозяйственных процессов деятельности предприятия. Таким образом, можно рассматривать данные, которые относятся не только к плановому и фактическому значениям, но и рассчитать факторное влияние для любых составляющих заданной модели. Важным является преобразование полученной динамической постановки задачи анализа конечных изменений к уже известной – статической, используя средневзвешенные (усредненные) значения факторов.