В [1] был описан метод векторной оптимизации выбора микроконтроллера (МК) с использованием аппарата нечетких множеств. Было отмечено, что на конечный результат сильно влияет способ задания экспертом функций принадлежности (ФП). В настоящей работе предлагается в общем виде метод, опирающийся на информацию об алгоритме и времени его выполнения, позволяющий на этапе анализа технических требований к МК уйти от субъективизма при построении функций принадлежности.
Очевидно, что этап определения технических требований, в частности значения тактовой частоты МК оказывает сильное влияние на результат выбора модели МК. В связи с чем, разработка метода оценки временной сложности алгоритма представляется весьма актуальной.
Переход от оценки асимптотической сложности алгоритма к временной оценке сопряжен с некоторыми объективными трудностями [4]: необходимость учёта особенностей используемого компилятора; различные времена выполнения реальных машинных команд; различие во времени выполнения одной команды в зависимости от значений операндов.
В настоящей работе для получения временных оценок предлагается использовать информацию по затратам машинного кода и числу тактов, необходимых для реализации операторов языка высокого уровня, полученную на основе статистических данных по частоте их употребления в типовых программах логического и цифрового употребления, где МК применяется наиболее широко [4], или же полученную после анализа алгоритма.
Предлагаемый метод включает в себя последовательность шагов:
1) разбиение программного алгоритма на конфигурационную и функциональную части;
2) определение количества высокоуровневых операций различных типов;
3) расчет количества тактов необходимых для реализации алгоритма с учетом имеющейся статистической информации по высокоуровневым операциям;
4) построение функции принадлежности частного критерия.
На рис. 1 представлена схема разрабатываемого метода.
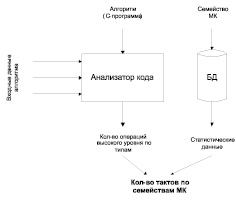
Рис. 1. Схема метода определения временных оценок алгоритма
Итак, программный алгоритм может быть разбит на две части: конфигурационную и функциональную. Нас в большей степени интересует функциональная часть, претендующая на многократное повторение. При таком подходе анализируемый алгоритм не будет привязан к конкретному МК, не будет зависеть от среды, и мы имеем полное право делать априорные оценки о времени выполнения алгоритма для любого МК.
После того, как функциональная часть алгоритма выделена, определяем количество высокоуровневых операций различных типов. В [4] предлагается использовать следующие элементарные операции:
1) простое присваивание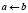 
;
2) одномерная индексация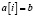 
;
3) арифметические операции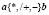 
;
4) операции сравнения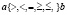 
;
5) логические операции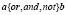 
;
6) операции адресации в сложных типах данных (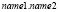
).
Рис. 1 отражает ситуацию, когда программный алгоритм задан в виде C-кода. Анализатор представляет собой программу, которая принимает на входе программный код и входные параметры алгоритма и рассчитывает кол-во высокоуровневых операций методом пооперационного анализа.
Основными алгоритмическими конструкциями являются конструкции следования, ветвления и цикла. С учетом введенных элементарных операция анализ таких конструкций сводится к следующим положениям.
а) конструкция «Следование». Трудоемкость конструкции есть сумма трудоемкостей блоков, следующих друг за другом
;
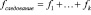б) конструкция «Ветвление». Общая трудоемкость конструкции «Ветвление» для построения функции трудоемкости в среднем случае требует анализа для получения вероятности p выполнения переходов на блоки «then» и «else»
;
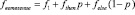в) Конструкция «Цикл по счетчику». После сведения конструкции к введенным операциям, ее трудоемкость определяется следующим образом
;
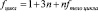Перед этапом анализа кода необходима подготовка экспериментальных данных. Сначала задаются возможные интервалы для всех входных переменных, и далее выбирается набор входных данных для проведения эксперимента. В базе данных хранится статистическая информация о том, сколько тактов требуется для реализации высокоуровневой операции в зависимости от типов данных. Такую информацию достаточно иметь для каждого семейства МК, а не для каждой модели.
Итак, из n входных наборов данных мы получим k возможных значений требуемых тактов x, при этом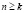 
. Количество тактов рассчитывается для каждого набора данных. Таким образом, после анализа алгоритма мы будем иметь множество возможных значений количества тактов X. Известно требуемое время выполнения алгоритма и время одного такта, множеству X ставится в соответствие множество возможных требуемых значений тактовой частоты для каждого МК V. Если наборы входных данных равновероятны, то с полученными данными предлагается работать следующим способом. Каждому событию появления значения 
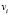ставится в соответствие вероятность р
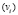. После ранжирования возможных значений тактов по возрастанию вероятностей становится возможным построение гистограммы вероятностей и, далее, функции плотности дискретной случайной величины, которая и будет являться нечеткой ФП частного критерия.
Приведем пример построения функции принадлежности по итогам анализа алгоритма. Предположим, что после 10 экспериментов с различными входными наборами были определены требуемые тактовые частоты МК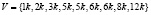 
, где k – некий условный коэффициент.
Построим гистограмму вероятностей появления каждого события (рис.2). После этого мы можем построить функцию принадлежности, которая являет собой функцию распределения дискретной случайной величины (рис. 3). На практике часто бывает достаточно s-образной функции принадлежности построенной по двум точкам для наилучшего и наихудшего случаев. Ниже приведен пример такой функции, построенной с учетом полученных результатов (рис. 4).
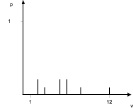
Рис. 2. Гистограмма вероятности
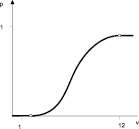
Рис. 3. Функция плотности распределения дискретной случайной величины
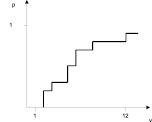
Рис. 4. Функция принадлежности критерия «тактовая частота»
Может возникнуть ситуация, когда на этапе выбора МК алгоритм не может быть задан C-программой. Если известно общее число высокоуровневых элементарных операций, то число конкретных операций может быть получено на основе статистических данных по частоте их употребления в типовых задачах. Тогда будет определено одно единственное значение количества требуемых тактов и значение требуемой тактовой частоты v, т.е. ФП для частного критерия может быть задана нечетким неравенством «тактовая частота примерно больше v». Однако следует отметить, что чем больше степень формализации алгоритма на данном этапе, тем более точно могут быть заданы требования к техническим параметрам МК.
В работе показана актуальность разработки метода оценки временной сложности алгоритма на этапе определения требований к МК. Описаны этапы построения ФП частного критерия на основе имеющейся информации по алгоритму.