В настоящий момент времени, в связи с появлением крупных зданий со сложной структурой, обозначилась проблема ориентации в таких местах. Для решения этой проблемы можно применять автоматические средства навигации внутри зданий, рынок которых в настоящий момент недостаточно развит.
Постановка проблемы
В системах подобного рода обязательным элементом являются функции для определения оптимального пути между двумя возможными местоположениями – текущим положением пользователя и целевым. Для реализации этой функции разработан целый класс алгоритмов для поиска кратчайшего пути. Один из таких алгоритмов – А*, который отличается от прочих наибольшим быстродействием, т.к. он выполняет поиск оптимального пути только между одной парой местоположений – начальным и конечным. Большинство других алгоритмов выполняют поиск либо между заданной текущим местоположением и всеми остальными, либо между каждой возможной парой местоположений. Поэтому быстродействие таких алгоритмов, особенно для зданий с большим количеством возможных местоположений, может быть далеко от оптимального.
Целью данной работы является практическая реализация алгоритма А* для поиска путей в трёхмерных структурах.
Представление входных данных
Обычно для алгоритмов поиска оптимальных путей входные данные представляются в виде взвешенного ориентированного графа, вершины которого соответствуют различным возможным местоположениям, а веса рёбер – точной оценке затрат на перемещение между ними (если прямой переход между какой-то парой вершин невозможен, то вес соответствующего ребра принимается равным бесконечности). Но для алгоритма А* одного графа недостаточно, т.к. алгоритм опирается на эвристическую (предположительную) оценку длины кратчайшего пути.
Вместо задания для алгоритма двух графов, ему можно сообщить информацию в более общем виде и дополнить алгоритм средствами динамической генерации этих двух графов. Возможный вариант данного представления состоит из следующих данных, находящихся во входном файле:
• n – количество возможных местоположений, задано как целое число;
• описание каждого местоположения, состоящее из названия (строка текста) и координат в трёхмерном пространстве (три целых числа);
• квадратная матрица размера n x n, составленная из булевых значений, в которой элемент с индексами (i, j) означает возможность прямого перемещения из местоположения i в местоположение j.
Реализация алгоритма с учетом вышеуказанных исходных данных производится следующим образом. После считывания данных из файла и получения от пользователя номеров начального и конечного местоположения, производится вычисление оценки по формуле (1) для каждого местоположения, в которое можно перейти их текущего за один проход.
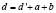, (1)
где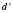 
– длина уже пройденного пути; а – расстояние до нового предполагаемого местоположения, вычисляется динамически как расстояние по прямой линии с учётом координат, указанных во входном файле; b – расстояние по прямой от предполагаемого нового местоположения до целевого (эвристическая оценка длины оставшегося пути), вычисляется аналогично.
Наиболее оптимальным выбором считается местоположение с наименьшим значением вычисленной оценки. После выбора следующего местоположения, происходит обновление длины пройденного пути. Новое значение вычисляется по формуле 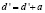(2).
. (2)
Кроме данных о возможных местоположениях, во входном файле также содержится полная информация для трёхмерной визуализации модели здания: имя файла текстуры, количество полигонов, трёхмерные координаты вершин каждого полигона, нормали и текстурные координаты.
Представление выходных данных
Интерфейс программной реализации состоит из двух элементов. Первый элемент – это информативное окно, с помощью которого производится выбор начального и конечного местоположений, вывод построенного маршрута и его длины и выбор этажа в модели здания для просмотра. Визуализация трёхмерной модели здания, возможных путей перемещения в здании и маршрут, построенный с помощью алгоритма, происходит во втором окне. Модель здания визуализируется с возможностью просмотра одного этажа, выбор которого производится в первом окне. Необходимо отметить, что построение множества возможных этажей производится на основе описания возможных местоположений: каждый этаж представляет собой высоту (вторая координата в трёхмерном пространстве), на которой находится как минимум одно возможное местоположение в здании. Таким образом, нет необходимости введения дополнительных входных данных.
Направление для дальнейших исследований
Данный метод формального описания возможных путей перемещения предполагает, что затраты на передвижение по пути прямо пропорциональны его длине, что не всегда верно. Некоторые технические средства (лифты, эскалаторы) позволяют преодолеть большое расстояние с небольшими затратами. Подобные случаи в предложенном методе не предусмотрены, поэтому в дальнейших исследованиях следует выполнить поиск решений этой проблемы.
Также, в дальнейшем следует реализовать новые методы визуализации модели здания, среди которых возможен обзор помещений здания изнутри с видом от первого лица. Текущий метод визуализации более всего близок к двумерным картам и не раскрывает потенциала трёхмерной визуализации.
Выводы
В данной работе осуществлена практическая реализация алгоритма поиска оптимального маршрута А* на языке C#, применительно к структурам, существующим в трёхмерном пространстве, с компактными входными данными и динамической генерацией рабочих данных для работы алгоритма и представлен формат записи входных данных.