Электролитическая цепь, в которой образуется ток, всегда состоит из проводника первого рода и проводника второго рода — электролита.
Дело в том, что в проводниках второго рода, в отличии от проводников первого рода, существуют два силовых поля. Одно поле образовано под действием электростатических сил Е, другое – под действием сторонних сил Естор (пондероматорных). Энергетический баланс (основной закон сохранения и превращения энергии) может быть удовлетворен только при условии равенства этих сил!
Молекулярно-кинетическая теория – основа расчета энергии необходимой для вырывания электрона или переноса энергии одного атома к другому.
Реакции, которые идут в различного рода электролитических элементах, дают примерно одно и тоже число джоулей на каждый отдельный акт химического взаимодействия между частицами (т. е. одинаковое число джоулей на элементарный заряд). В большинстве случаев около 1·10-19 или 2·10-19 дж на элементарный заряд. Поэтому с практической точки зрения удобно принимать за единицу ЭДС такую же величину. Эта величина и называется Вольтом, т. е. 1В=1,6·10-19 дж/элем. заряд. Энергия необходимая для вырывания электрона или переноса от одного атома к другому, приблизительно равна 1 вольту, умноженному на элементарный заряд. Именно поэтому за единицу измерения энергии принят электрон-вольт. Электрон-вольт пригоден для измерения энергии «химических реакций» между отдельными частицами и энергий, требуемых для ионизации отдельных атомов. Тогда, если мы приняли за единицу энергии 1В=1,6·10-19 дж/элем. заряд, то за единицу заряда необходимо ввести новую единицу, например кулон так, чтобы произведение одного кулона на ЭДС в один вольт дало один джоуль 1 кулон·1 В=1 дж, тогда 1кулон=1 дж/1В=1,6·10-19 дж/элем. заряд=6,25·1018 элем. зарядов. При таком выборе единиц заряда сила тока является ампером, поэтому 1А=6,25·1018 элем. зарядов за секунду. В проводниках первого рода переносчиками заряда являются электроны, а в проводниках второго рода – ионы. Ток, как было выше отмечено, есть результат взаимодействия электромагнитной энергии IE c веществом, есть замкнутая субстанция и представляет собой непрерывное течение электрического заряда. Поэтому на границе полей (проводников) происходят превращения: на аноде анионы должны отдавать лишние электроны и превращаться в нейтральные атомы, а на катоде, наоборот, катионы получать электроны и превращаться в нейтральные атомы. Только в этом случае суммарный ток в электролите будет равен электронному току в металлической части цепи. Однако это явление сопровождается химическим разложением электролита и, следовательно, скорости, электропроводимость и другие параметры в проводниках второго рода будут зависеть от степени химического разложения (названной диссоциацией) электролита, и величины суммарного электрического поля Е+Естор [1].
На основании выше изложенного, составим молекулярно-кинетическую схему движения ионов в электролите (анионов и катионов), (рис. 1). 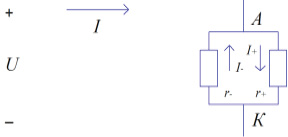
Рис.1 Молекулярно-кинетическая схема движения ионов в электролите
Как видим, ток в электролитах обеспечивается одновременным встречным движением положительно и отрицательно заряженных ионов под воздействием суммарного электрического поля. Напряжение U в электродной системе анод-катод одно и тоже и для сопротивления r+, положительно заряженных ионов, и для сопротивления r-, отрицательно заряженных. Особо отметим, поскольку движение зарядов противополярное и одновременное, то молекулярно-кинетические скорости этих движений складываются, а образовавшийся ток, одновременным противополярным движением ионов, характеризуется их среднеквадратичной скоростью. Направление движения положительно заряженных ионов совпадает с направлением электронного тока. 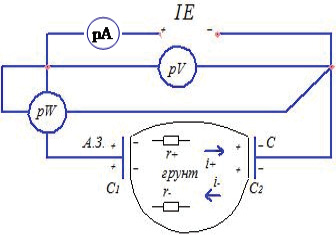
Рис. 2. Принципиальная электрическая схема движения элементарных частиц
Поэтому поток положительно заряженных ионов принимаем за электронный ток, ток, измеряемый амперметром- I+. Ток, образованный отрицательно заряженными ионами, обозначим- I-. Таким образом, амперметр, включенный в электродную электрическую цепь (рис. 2), фиксирует электронный ток. Вольтметр фиксирует падение напряжения, на разных по величине сопротивлениях r+ и r-, другими словами – разность падений напряжений. Таким образом, генерируемая энергия в электродной электрической цепи оказалась связанной с энергией и количеством движения заряженных микрочастиц ионов, движущихся в противоположных направлениях. А поскольку произведение силы тока на ЭДС (IE) удовлетворяется только тогда, если измерять числом элементарных зарядов, переносимых за секунду, а ЭДС джоулями на элементарный заряд, то можно по данным прямых измерений вольтметром и ваттметром, рассчитать величину тока при определенной мощности в любой электролитической системе: IE=PW=U·1,65·10-19·I·6,25·1018 (Вт·с), тогда I= PW/U·1,65·10-19·6,25·1018 (А).
Естественно, этот ток I не может быть равен току измеряемого амперметром, включенного в электролитическую цепь (рис. 2).
Назовем этапы, законы которые использованы для получения нового этапа, нового видения закономерностей образования электрического тока в проводниках второго рода:
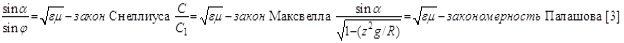
Математическая модель молекулярно-кинетического взаимодействия постоянной или выпрямленной ЭДС с проводниками второго рода.
Взаимодействие электромагнитного поля со средой обусловлено исключительно заряженными частицами, независимо распределенными в теле или связанными в диполи [2]. Поэтому сила, действующая в электромагнитном поле на элемент объема среды, является результирующей пондероматорных сил на все находящиеся в данном объеме электрические и магнитные элементарные частицы.
Вектор Пойнтинга*1, деленный на с², представляет собой пространственную плотность импульса П/с²=mu, как объемную плотность силы (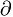 П/
П/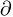 t)/с²=
t)/с²=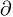 (mu)/
(mu)/ 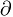 t [4].
t [4].
Представляя распространение потока электромагнитной энергии через границу раздела фаз металл-электролит в виде вектора Пойнтинга, нами получена формула (1) в [4, 5].
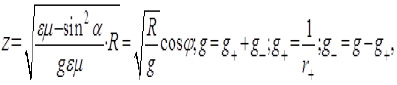 (1)
(1)
где z – кажущееся сопротивление; R – омическое сопротивление; g – общая проводимость;
εμ – показатель среды; α – угол распространения энергии; φ – угол преломления энергии;
g+ - проводимость анионов (1/r+); g- - проводимость катионов (1/r-).
Используя аналогию понятия закона Максвелла 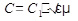 , закона Снеллиуса
, закона Снеллиуса 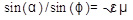 и выявленную автором формулу (2) в [6]:
и выявленную автором формулу (2) в [6]:
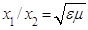 (2)
(2)
где х1, х2 – соответственно сопротивления анионам и катионам, находящихся в сложной зависимости от их масс, скоростей их движения и от дополнительных сил торможения: электростатических и релаксации.
Можно разработать математическую модель молекулярно-кинетического взаимодействия электромагнитной энергии с электролитами.
Для достижения результата преобразуем формулу (1), получим:
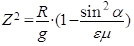 (3)
(3)
Перенесем неизвестные параметры, явно сложно поддающие практическому измерению, в левую часть уравнения (3):
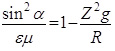 (4)
(4)
Извлечем корень квадратный из обеих частей уравнения:
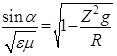 (5)
(5)
Тогда:
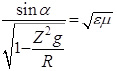 (6)
(6)
Сравним формулу закона Снеллиуса, Максвелла и полученную нами (6):
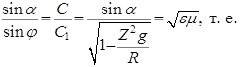 (7)
(7)
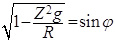 (8)
(8)
Принимая, как это видно из (7), sinα за параметр С, а 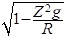 за С1, получим зависимости sinφ от измеряемых параметров:Z2, g, R, а также g+ и g-
за С1, получим зависимости sinφ от измеряемых параметров:Z2, g, R, а также g+ и g-
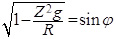 ;
;
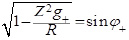 ;
;
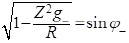 ,
,
а поскольку (7):
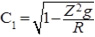 , легко понять
, легко понять
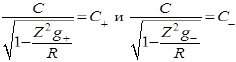 , где
, где
С+ - кинетическая скорость движения анионов;
С- - кинетическая скорость движения катионов;
С – скорость течения движения в вакууме, С++С-=С.



