Физическая постановка задачи [1] позволяет, в соответствии с принятыми допущениями, приступить к этапу синтеза математической модели. Для этого выделим элементарный объем и запишем для него дифференциальное уравнение материального баланса
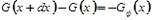, (1)
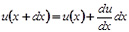, (2)
с очевидным начальным условием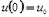 
.
Материальный баланс по частицам в суспензии для элементарного объема в дифференциальной форме
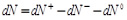, (3)
где dN – изменение числа частиц в элементарном объеме; dN+ – число частиц входящих в элементарный объем; dN- – число частиц покидающих элементарный объем; dN0 – число частиц, осевших или профильтровавшихся через пористую стенку.
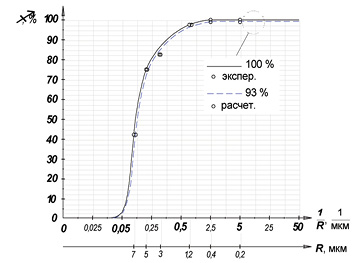
Рис. 1. Зависимость селективности от размера пор мембраны
После математических преобразований
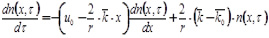(4)
с очевидными краевыми условиями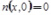 
, 
.
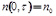В итоге
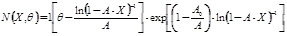, (5)
Обобщение решения (5) можно получить суперпозицией концентрационных полей. Для фракции с размерами частиц от l до ∆l запишем
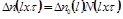. (6)
А вводя безразмерные переменные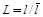 
; 
; 
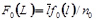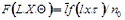относительная массовая концентрация примесей на выходе из фильтра
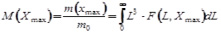, (7)
где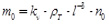 
– массовая концентрация частиц на входе в фильтр.
Сравнительный анализ расчетных и экспериментальных данных [1] показал хорошую сходимость: отклонение расчетных от экспериментальных данных не превышало 17 %.