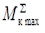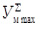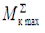Применяемые в настоящее время для обработки почвы машины с активными ротационными рабочими органами, обладают небольшим тяговым сопротивлением, что позволяют существенно снизить металлоемкость, как самой машины, так и всего агрегата при неизменной мощности двигателя [1]. Однако при этом указанные машины имеют недостаточную надежность и малую долговечность. Поэтому определение оптимальных конструктивных параметров рабочих органов и наиболее приемлемых кинематических режимов их работы, изучение закономерностей динамических процессов и выявление зависимостей между ними является первостепенной задачей, решение которой способствует дальнейшему усовершенствованию конструкции, повышению надежности, долговечности и функционирования этих машин [2, 3, 4].
Предлагаемый материал посвящен анализу динамических нагрузок в приводе машины для глубокого вскапывания и предпосадочной обработки почвы в теплицах МПТ-1,2 (рис. 1) заключающегося в определении коэффициента неравномерности угловой скорости на приводном валу ее рабочего органа (фрезбарабана).
|
|
|
Рис. 1. Машина для обработки почвы в теплицах МПТ-1,2 |
Для решения поставленной задачи были использованы аналитические методы, основанные на применении уравнений кинетической энергии [5, 6]. При этом динамический анализ фрезбарабана проводился за один рабочий цикл, принятый равным одному полному его обороту при условии установившегося протекания технологического процесса фрезерования почвы. В качестве объекта обработки являлся малогумусный чернозем с плотностью почвы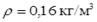 
. Кроме того, учитывались конструктивные и технологические особенности машины, а в частности конструкция фрезбарабана состоящего из 5 рабочих секций с 32 Г-образными ножами (табл. 1) и рабочий угол резания почвы.
Таблица 1
Размещение ножей по дискам и последовательность их работы
|
Номер диска |
Номер ножа |
Угловой шаг β, градус |
Номер ножа |
Угловой шаг β, градус |
||||
|
1 |
2 |
3 |
4 |
5 |
||||
|
Номер ножа |
13 |
17 |
17 |
198 |
||||
|
1 |
5 |
13 |
21 |
29 |
29 |
32 |
31 |
212 |
|
2 |
6 |
14 |
22 |
30 |
5 |
39 |
9 |
220 |
|
3 |
7 |
15 |
23 |
31 |
14 |
45 |
18 |
226 |
|
4 |
8 |
16 |
25 |
32 |
21 |
56 |
25 |
235 |
|
– |
10 |
18 |
26 |
– |
6 |
66 |
10 |
245 |
|
– |
11 |
19 |
27 |
– |
22 |
82 |
26 |
262 |
|
– |
12 |
20 |
28 |
– |
2 |
90 |
4 |
270 |
|
– |
– |
– |
– |
– |
15 |
107 |
19 |
288 |
|
– |
– |
– |
– |
– |
30 |
121 |
32 |
302 |
|
– |
– |
– |
– |
– |
7 |
127 |
11 |
208 |
|
– |
– |
– |
– |
– |
16 |
135 |
20 |
316 |
|
– |
– |
– |
– |
– |
23 |
144 |
27 |
324 |
|
– |
– |
– |
– |
– |
8 |
155 |
12 |
335 |
|
– |
– |
– |
– |
– |
24 |
172 |
28 |
353 |
|
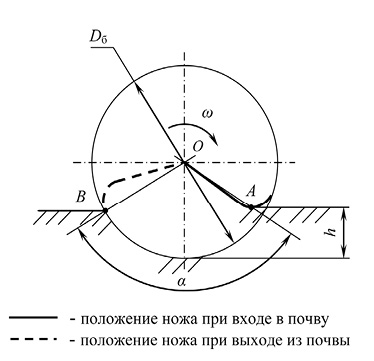
Рис. 2. Схема для определения рабочего угла ножа |
Рабочий угол резания почвы одного ножа α (градус) вычисляли при максимальной глубине обработки h = 20 см. Для этого строили расчетную схему (рис. 2), откуда получили, что α = 1700 .
На первом этапе анализа динамических нагрузок в приводе машины определяли изменение крутящего момента на приводном валу от угла поворота фрезбарабана как для оного ножа, так для всего фрезбарабана. При этом максимальное значения крутящего момента на приводном валу для одного ножа определяли из выражения [6]:
,
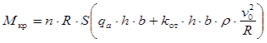где п – количество ножей, п = 1; r0 – радиус барабана, м; R = 0,4 м; S – подача на нож, м; S = 0,14 м; qа – коэффициент объемного смятия, qа = 0,6 . 106 Н/м3; b – ширина захвата ножа, м; b = 0,125 м; kот – коэффициент отбрасывания,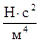 
; kот= 0,85 
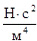; h – глубина обработки, м; h = 0,2 м; ρ – плотность почвы, кг/м3; ρ = 0,16 кг/м3; v0 – окружная скорость на лезвии ножа, м/с; v0= 3,12 м/с.
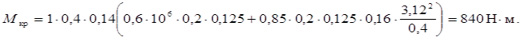
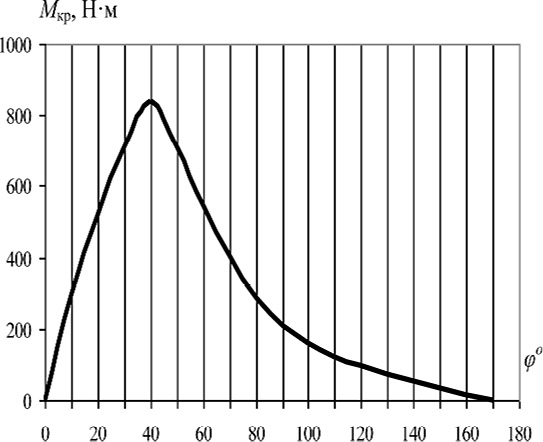
Используя кривую изменения приводного момента за рабочий ход для Г-образных ножей [7] и полученное значение Мкр строим соответствующий график (рис. 3).
Далее используя данные таблицы 1 и рис. 3, путем последовательного сложения ординат диаграмм, построенных с угловым сдвигом, равным угловому шагу ножей β, строим суммарный график крутящего момента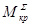 
, Н·м (рис. 4), откуда находим значения минимальной и максимальной амплитуды крутящего момента на приводном валу фрезы: Мкр.min = 4009 Н. м и Мкр.max = 4742 Н. м.
|
|
|
Рис. 3 Диаграмма изменения крутящего момента на валу фрезбарабана |
Рис. 4. Диаграмма изменения суммарного крутящего момента
Для дальнейших графических построений определим масштабы построения для суммарного графика крутящих моментов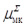 
и угла поворота фрезбарабана 
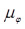по формулам:
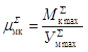и 
,
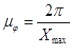где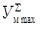 
– высота ординаты наибольшего значения суммарного момента, мм; принимаем 
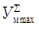= 235 мм; Хmax – длина отрезка отображающего угол поворота фрезбарабана на 360о, мм; принимаем Хmax = 180 мм.
С учетом принятых значений получаем:
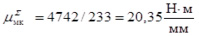и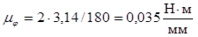 
.
Поделив значения суммарных крутящих моментов на величину масштаба, определим ординаты для построения диаграммы. Результаты расчетов приведены в таблице 2.
Таблица 2
Значения суммарных крутящих моментов
|
φ, градус |
мм |
Н .м |
φ, градус. |
мм |
Н .м |
φ, градус |
мм |
Н.м |
|
0 (360) |
233 |
4742 |
120 |
207 |
4212 |
240 |
207 |
4212 |
|
10 |
231 |
4701 |
130 |
200 |
4070 |
250 |
215 |
4375 |
|
20 |
220 |
4477 |
140 |
208 |
4233 |
260 |
223 |
4538 |
|
30 |
202 |
4111 |
150 |
210 |
4274 |
270 |
228 |
4640 |
|
40 |
197 |
4009 |
160 |
211 |
4294 |
280 |
233 |
4742 |
|
50 |
202 |
4073 |
170 |
228 |
4640 |
290 |
220 |
4477 |
|
60 |
207 |
4212 |
180 |
233 |
4742 |
300 |
207 |
4212 |
|
70 |
215 |
4375 |
190 |
231 |
4701 |
310 |
200 |
4070 |
|
80 |
223 |
4538 |
200 |
220 |
4477 |
320 |
208 |
4233 |
|
90 |
228 |
4640 |
210 |
202 |
4111 |
330 |
210 |
4274 |
|
100 |
233 |
4742 |
220 |
197 |
4009 |
340 |
211 |
4294 |
|
110 |
220 |
4477 |
230 |
202 |
4073 |
350 |
228 |
4640 |
Затем графическим интегрированием диаграммы моментов строим диаграмму работ полезных сил сопротивления Ас = Ас(φ). Построение диаграммы работ движущих сил Ад = Ад(φ) производим с допущением, что движущий момент постоянен во времени, т.е. Мд = const. Тогда график работы движущих сил будет представлять наклонную прямую, соединяющую точку С диаграммы Ас = Ас(φ) с началом координат (рис. 5).
Масштаб диаграммы работ определим из соотношения:
,
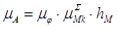где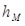 
– полюсное расстояние, мм; 
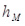= 250 мм.
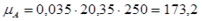Дж/мм.
Вычитая ординаты работы сил полезных сопротивлений из ординат работы движущих сил для каждого положения фрезбарабана, построим диаграмму изменения кинетической энергии от угла поворота ножей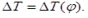 
Выбираем масштаб построения:
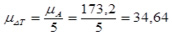Дж/мм.
Вычислим остальные ординаты по формуле:
.
Результаты расчетов приведены в таблице 3. По полученным данным построим диаграмму изменения кинетической энергии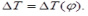 
(рис. 6).
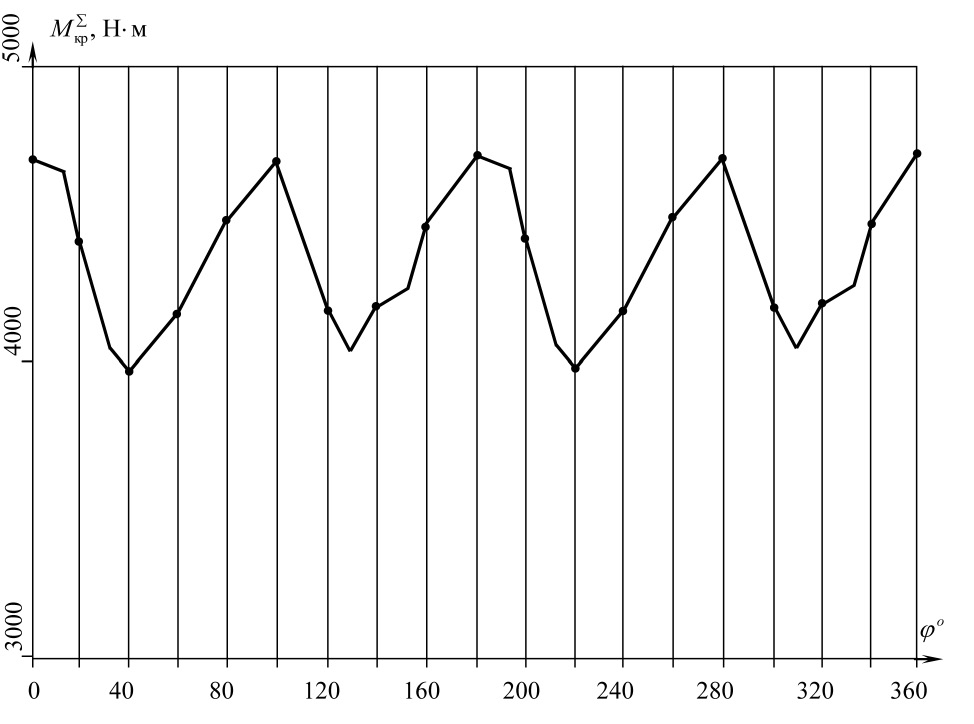
Рис. 5. Диаграммы изменения работ полезных сил сопротивления Ас = Ас (φ) и движущих сил Ад = Ад(φ)
Таблица 3
Кинетическая энергия на валу фрезбарабана и ее ординаты
|
φ, градус |
ΔТ, Дж |
УΔТ, мм |
Тi, Дж |
УТi, мм |
ΔТ ', Дж |
УΔТ', мм |
|
0 (360) |
0 |
0 |
252,5 |
7,3 |
252,5 |
-7,3 |
|
20 |
346,4 |
-10 |
252,5 |
7,3 |
599,3 |
-17,3 |
|
40 |
173,2 |
-5 |
252,5 |
7,3 |
426 |
-12,3 |
|
60 |
207,8 |
-6 |
252,5 |
7,3 |
4607 |
-13,3 |
|
80 |
207,8 |
-6 |
252,5 |
7,3 |
460,7 |
-13,3 |
|
100 |
346,4 |
-10 |
252,5 |
7,3 |
599,3 |
-17,3 |
|
120 |
519,6 |
-15 |
252,5 |
7,3 |
772,4 |
-22,3 |
|
140 |
519,6 |
-15 |
252,5 |
7,3 |
772,4 |
-22,3 |
|
160 |
519,6 |
-15 |
252,5 |
7,3 |
772,4 |
-22,3 |
|
180 |
1385,6 |
-40 |
252,5 |
7,3 |
1638 |
-47,3 |
|
200 |
1732 |
-50 |
252,5 |
7,3 |
1985 |
-57,3 |
|
220 |
1420,2 |
-41 |
252,5 |
7,3 |
1673 |
-48,3 |
|
240 |
1385,6 |
-40 |
252,5 |
7,3 |
1638 |
-47,3 |
|
260 |
1247 |
-36 |
252,5 |
7,3 |
1500 |
-43,3 |
|
280 |
1039 |
-30 |
252,5 |
7,3 |
1292 |
-37,3 |
|
300 |
866 |
-25 |
252,5 |
7,3 |
1119 |
-32,3 |
|
320 |
554 |
-16 |
252,5 |
7,3 |
807 |
-23,3 |
|
340 |
173,2 |
-5 |
252,5 |
7,3 |
426 |
-12,3 |
Рис. 6. Диаграмма изменения кинетической энергии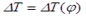 
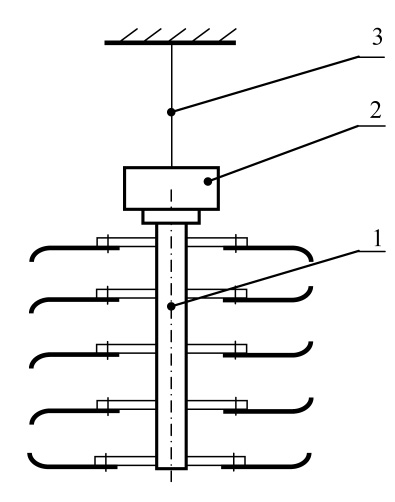
Далее методом крутильных колебаний определяем момент инерции фрезбарабана относительно собственной оси вращения, для чего фрезбарабан 1 закрепляем в патроне 2 подвешенному на упругом стальном стержне 3 лабораторной установки (рис. 7).
Затем после проведения серии опытов, определяем значение момента инерции фрезбарабана по формуле:
,
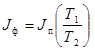где Jф и Jп – моменты инерции фрезбарабана и патрона, кг·м2; Т1 и Т2 – периоды крутильных колебаний для патрона и фрезбарабана соответственно, с.
В результате проведения опытов и расчетов получаем: Jф = 8,3 кг·м2.
Перепад кинетической энергии определяем методом Мерцалова-Рериха [], для чего вычисляем кинетическую энергию фрезбарабана и строим диаграмму 
в том же масштабе, в котором построена диаграмма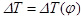 
.
Кинетическую энергию фрезбарабана при его угловой скорости ωф = 7,8 рад/с определим по формуле:
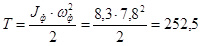Дж
Рис. 7. Схема установки для определения момента инерции фрезбарабана методом крутильных колебаний
Определяем ординату диаграммы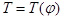 
:
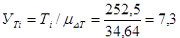мм.
По ординатам, приведенным в таблице 3, строим диаграмму изменения кинетической энергии фрезбарабана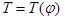 
и дополнительную диаграмму 
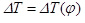(рис. 8 и 9), при этом абсолютные значения последней определяем из соотношения 
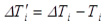, а ее ординаты вычисляем из выражения 
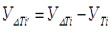. Результаты расчетов приведены в таблице 3.
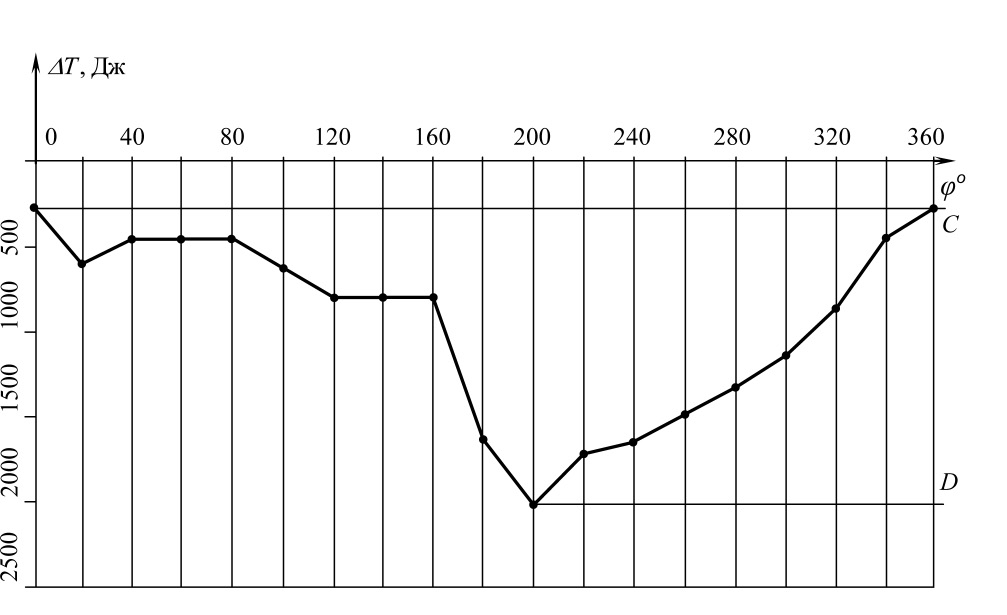
На диаграмме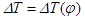 
(рис. 9) проведем горизонтальные прямые к экстремальным точкам функции. Эти прямые пересекут ось ординат в точках С и D. Полученный отрезок СD = 50 мм будет выражать в масштабе 
размах колебаний кинетической или избыточной энергии.
Рис. 8. Диаграмма изменения кинетической энергии фрезбарабана 
Рис. 9. Дополнительная диаграмма изменения кинетической энергии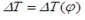 
Для определения значений угловой скорости на валу фрезбарабана ωф воспользуемся данными таблицы 3 и формулой:
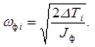
Результаты вычислений представлены в таблице 4.
Далее определяем величины ординаты Уω (мм) диаграммы изменения угловой скорости фрезбарабана по формуле:
,
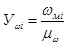где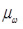 
– масштаб построения диаграммы изменения угловой скорости фрезбарабана, 
.
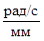Значение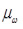 
определим по формуле:
,
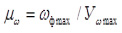где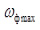 
– максимальное значение угловой скорости фрезбрабана, рад/с; согласно данным таблицы 4 –
; 
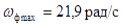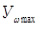– максимальная величина ординаты графика, мм; принимаем 
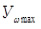= 100 мм.
Тогда
.
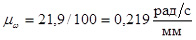Результаты расчета ординат Уω представлены в таблице 4, а диаграмма изменения угловой скорости ωф = ωф (φ) на рис. 10.
Таблица 4
Значения угловых скоростей и их ординат
|
φ, градус |
ΔТ, Дж |
ωф, рад/с |
Уω, мм |
φ, градус |
ΔТ, Дж |
ωф, рад/с |
Уω, мм |
|
0 (360) |
252,5 |
7,8 |
35,6 |
180 |
1638,0 |
19,9 |
90,9 |
|
20 |
599,3 |
12,0 |
54,7 |
200 |
1985,0 |
21,9 |
100,0 |
|
40 |
426,0 |
10,1 |
46,1 |
220 |
1673,0 |
20,1 |
91,7 |
|
60 |
460,7 |
10,5 |
47,9 |
240 |
1638,0 |
19,9 |
90,9 |
|
80 |
460,7 |
10,5 |
47,9 |
260 |
1500,0 |
19,0 |
86,8 |
|
100 |
599,3 |
12,0 |
54,8 |
280 |
1292,0 |
17,6 |
80,4 |
|
120 |
772,4 |
13,6 |
62,1 |
300 |
1119,0 |
16,4 |
74,9 |
|
140 |
772,4 |
13,6 |
62,1 |
320 |
807,0 |
13,9 |
63,5 |
|
160 |
772,4 |
13,6 |
62,1 |
340 |
426,0 |
10,1 |
46,1 |
Из диаграммы изменения угловой скорости приводного вала фрезбарабана (рис. 10) получаем минимальное и максимальное значения угловой скорости, т. е.: ωф min =7,8 рад/с и ωф max = 21,9 рад/с. Затем определяем среднее значение угловой скорости приводного вала фрезы ωф ср и ее ординату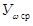 
на диаграмме, по соответствующим формулам:
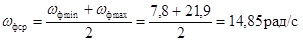и 
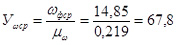мм.
По полученным данным строим диаграмму угловой скорости ωфср= ωфср(φ) (рис. 10).
После чего, определяем расчетный коэффициент неравномерности угловой скорости по формуле:
.
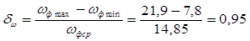Рис. 4. Диаграмма изменения угловой скорости приводного вала фрезбарабана
Из сравнения полученного значения δω с допускаемым [δ] = 0,2 [6], следует, что расчетное значение коэффициента δω превышают допускаемое в 4,75 раза, что отрицательно сказывается на надежности и долговечности элементов привода не только фрезы, но и привода вала отбора мощности энергетического средства и на загрузке его двигателя, а также на качестве обработки почвы. Поэтому необходимы конструкторские и технологические решения по устранению причин, вызывающих значительную неравномерность крутящего момента и угловой скорости на приводном валу рабочих органов почвообрабатывающей фрезы.