Теория удара, в своей основе, опирается на представление о коэффициенте восстановления, восходящее к И. Ньютону. Это понятие применяется в разнообразных инженерных расчетах. Однако эксперименты и теоретические изыскания в пределах теории упругости не совсем точно согласуются с известным представлением И. Ньютона о том, что коэффициент восстановления при соударении упругих тел равен единице. Настоящая статья носит характер аналитического обобщения различных подходов к обозначенной теме.
Основные проблемы при теоретическом описании явления удара вызваны широтой исследуемых явлений. Могут быть неизвестны как силы, действующие во время удара, так и свойства материалов соударяющихся тел. В зависимости от цели, поставленной при решении задачи, может потребоваться определить конечные состояния материальных объектов, силы, действующие при ударе или другие характеристики исследуемого процесса. Однако в большинстве случаев инженерных расчетов чаще всего подлежат определению силы, возникающие в процессе удара. При этом, как правило, рассматриваются одномерные и плоские задачи как наиболее часто встречающиеся в теории удара [1].
Для характеристики удара используют интегральную величину – ударный импульс
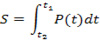
Здесь t0 и t1 – время начала и конца удара, P(t) – сила, возникающая во время удара. Применяя часто используемый в теоретической физике предельный переход t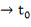
и дельта-функцию Дирака получим выражение для так называемой мгновенной ударной силы:
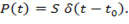
Мгновенный ударный импульс S считается бесконечно большой величиной.
Введение мгновенной ударной силы используется для проведения аналитического исследования проблемы в рамках классической механики. При этом объектом исследования выступает модель абсолютно твердого тела. Однако «довольно успешное» применение данной модели для описания общих законов движения и равновесия материальных объектов чаще всего дает неверные результаты в теории удара. Математически неприменимость модели абсолютно твердого тела выражается в том, что система уравнений, записанная, например, по закону сохранения импульса неразрешима – количество неизвестных больше числа уравнений для их определения.
Задача описать соударение упругих тел без введения их пластических свойств требует введения дополнительных предположений. Еще до теоретических представлений И. Ньютона об эффекте восстановления при соударении упругих тел такие дополнительные гипотезы были предложены Марци, Гюйгенсом и Валлис. Первое предположение состоит в неизменности кинетической энергии – величина относительной скорости в этом случае не изменяется при ударе. Второе – скорости взаимодействующих тел после удара равны.
Согласно предположению И. Ньютона разности скоростей до удара и после удара прямо пропорциональны.
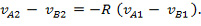
Коэффициент пропорциональности R был назван коэффициентом восстановления. Минус введен для того, чтобы коэффициент восстановления имел положительное значение при исследовании упругих деформаций.
Предположение Ньютона включило в себя в качестве предельных случаев оба указанных выше предположения – при R=0 конечные скорости тел A и B (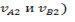
равны; при R=1 разности скоростей одинаковы. При этом оценка коэффициента восстановления осуществляется опытным путем посредством измерения скоростей тела на высоте отскока h2 при падении с высоты h1.
Для скоростей падающего тела до и после соударения запишем:
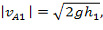
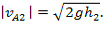
Тело, о которое происходит удар, покоится:
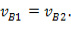
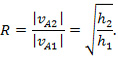
Совершенно очевидно, что оригинальная теория Ньютона основана только на кинематическом описании удара. Здесь отличие R от единицы считается вызванным пластическими деформациями на основе предположения локализации деформаций вблизи поверхности взаимодействующих объектов. Однако энергия может уходить не только в неупругие деформации, но и в упругие – например колебания. В этой связи термин «коэффициент восстановления» не отражает всех возможностей распределения и расходования энергии удара. Необходим анализ внутренней структуры системы тел, в которой происходит удар, то есть оценка коэффициента восстановления с точки зрения качественного рассмотрения динамики взаимодействия объектов. Данная процедура заключается в следующем.
Рассмотрим плоское движение двух тел. Разобьем процесс удара на две фазы. Первую назовем фазой нагрузки. В течение фазы нагрузки центры масс тел сближаются, относительная скорость падает до нуля, силы взаимодействия возрастают. В фазе разгрузки ударная сила спадает до нуля, скорости движения тел меняют знак на противоположный. На границе этих двух фаз тела находятся в плотном контакте, неподвижны друг относительно друга (их можно рассматривать как механическую систему) и движутся со скоростью центра масс данной системы тел
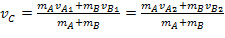
Импульс нагрузки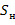 
можно выразить как величину импульса, на который изменится импульс первого тела с момента соприкосновения со вторым до конца фазы нагрузки:
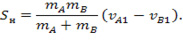
Аналогично можно ввести импульс разгрузки:
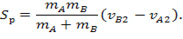
Тогда коэффициент восстановления R будет равен отношению импульса разгрузки к импульсу нагрузки:
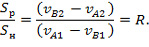
Вместе с тем, рассматривая соотношение между кинетической энергией частей системы до (T1) и после соударения (T2), так же можно определить коэффициент восстановления:
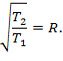
Используя данный подход к оценке R изменение кинетической энергии системы тел будет определяться так:
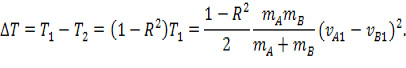
Экспериментальные исследования также показали, что R зависит и от относительной скорости соударения тел [2]. Эмпирическая формула зависимости коэффициента восстановления от относительной скорости соударяющихся тел имеет следующий вид:
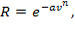
где a и n - экспериментально определяемые коэффициенты, v – скорость относительного движения тел в момент перед ударом. Использование этой эмпирической формулы сразу же делает исследование удара более сложным, чем в оригинальной теории Ньютона.
Проведенный анализ различных подходов к оценке коэффициента восстановления при соударении упругих тел, на наш взгляд, показал преимущества динамического подхода к его определению. Кинематическое описание удара не позволяет качественно рассмотреть эффект взаимодействия упругих тел при соударении, что вносит значительную погрешность в величину реального коэффициент восстановления R. Вместе с тем, совершенно очевидно, что в действительности коэффициент восстановления также зависит и от конкретных свойств веществ соударяющихся тел.