Теоретическая механика как фундаментальная классическая наука позволяет разрешить множество прикладных инженерных задач, сводящихся к расчету механизмов, сооружений, летательных аппаратов и т. п. методом построения их математических моделей. Одной из таких задач является исследование движения ступенчатого катка по такому же основанию. Для рассмотрения примем модель, изображенную на рисунке.
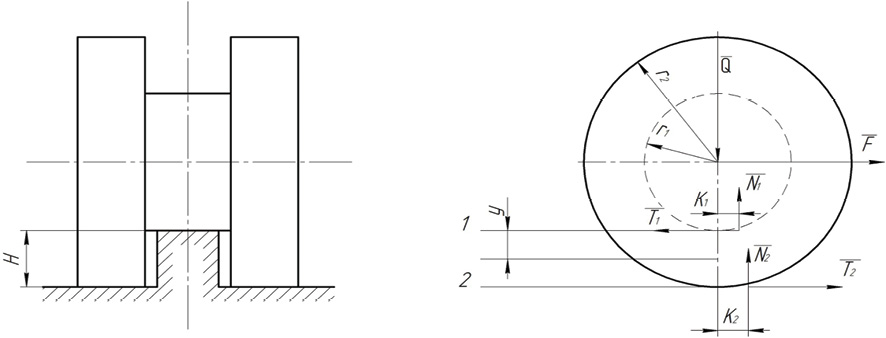
Пусть качение происходит под действием силы F, направленной вдоль горизонтальной оси и приложенной к оси катка, которая движется равномерно и прямолинейно. На каток действуют вертикальная нагрузка Q, реакции поверхностей основания N1 и N2 и силы трения на этих поверхностях Т1 и Т2. Из условия модели будем считать, что высота ступени основания равна разнице радиусов ступенчатого катка Н=r2-r1.
Чтобы определить условия гарантированного скольжения на поверхностях основания 1 или 2, рассмотрим движение катка вокруг мгновенной оси вращения. Данная ось располагается на вертикальном диаметре катка между поверхностями 1 и 2 на определенном расстоянии от первой поверхности (примем это расстояние за y). Так как ось катка движется равномерно, то и сам каток совершает установившееся движение. Значит сумма работ всех сил на любом возможном перемещении равна нулю и действительно равенство: 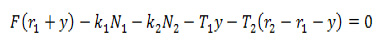
где k1 и k2 – коэффициенты трения качения на поверхностях оснований 1 и 2.
Рассматривая общий случай, где скольжение будет происходить на обеих поверхностях, имеем, что T1=f1N1, T2=f2N2 (f1 и f2 – коэффициенты трения скольжения на поверхностях 1 и 2 соответственно). Подставляем и решаем уравнение относительно F. Получим:
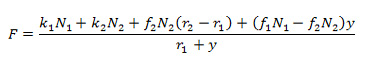
Обозначив постоянные

будем иметь:
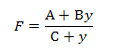
Величина движущей силы, таким образом, зависит от положения мгновенной оси вращения. Коэффициент В позволяет установить является эта зависимость прямой или обратной. Вместе с тем при некотором В=В0 величина силы будет неизменной, независимой от положения и постоянной.
На основании принципа стационарности действия Гамильтона при действительном движении катка затраты энергии на движение минимальны. Тем самым качение будет возможно при наименьшей cиле F. Это значит что при прямой зависимости силы от положения мгновенной оси вращения (В>B0) последняя будет расположена на поверхности 1(у=0), а при обратной (B<B0) – на поверхности 2(у=r2-r1). В то время как при В=В0 положение мгновенной оси вращения будет неопределенным.
В случае B=B0, как было сказано выше,
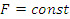 и
и 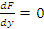 .
.
Тогда:
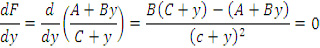
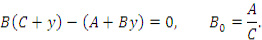
Для обеспечения скольжения на поверхности 1 необходимо выполнить условие B<B0:
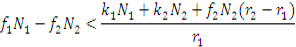
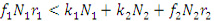 (1)
(1)
Чтобы скольжение происходило на поверхности 2 должно выполняться условие B>B0:
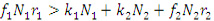 (2)
(2)
При обращенном движении, то есть когда ось катка закреплена, а ведущим звеном является ступенчатое основание, картина остается аналогичной. Регулируя величины, входящие в неравенства (1) и (2), можно осуществить желаемый режим движения катка или основания.



