Введение
Моделирование является важным этапом при исследовании и проектировании любой информационно-измерительной системы, в том числе бесплатформенной системы ориентации (БСО), являющейся частью инерциальной навигационной системы (БИНС). Современные средства компьютерного моделирования позволяют формировать математическую модель БСО, отслеживать работу системы в реальном масштабе времени, а также представлять результаты расчетов в наглядном и удобном для дальнейшего анализа виде. Среди множества программ математического моделирования выделяются программы Mathcad и Matlab. Данные программы имеют широкое распространение благодаря простоте обучения, вычислений и инженерных расчетов.
Одной из задач моделирования БСО является определение ее точностных характеристик с учетом погрешностей чувствительных элементов и внешних возмущений. Однако результаты, полученные при моделировании работы БСО, будут также включать в себя ошибки самой среды моделирования. Данные ошибки определяются численными методами, применяемыми в конкретной среде моделирования, и являются методической погрешностью вычислительного эксперимента.
В частности, вклад в общую погрешность вносит процедура дифференцирования, применяемая при моделировании работы БСО. Целью данной работы является оценка ошибки моделирования работы БСО при применении процедуры дифференцирования в программах Mathcad и Matlab.
Задачи работы:
1) сформировать программу моделирования;
2) провести численные эксперименты;
3) сделать заключение.
1 Математическая модель
БИНС включает в себя два основных блока [1]:
блок измерителей параметров поступательного и углового движения объекта (например, акселерометры и датчики угловой скорости);
вычислитель (включает в себя навигационный алгоритм и алгоритм ориентации).
Как известно, алгоритм БСО может быть реализован с использованием различных кинематических параметров, таких как углы Эйлера-Крылова, направляющие косинусы, параметры Кэли-Клейна и др. Выбор кинематических параметров определяется спецификой конкретной навигационной задачи. В данной работе рассматривается алгоритм БСО с углами Эйлера-Крылова.
Кинематические уравнения в углах Эйлера-Крылова имеют вид [1]:
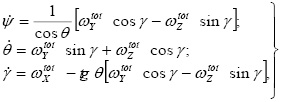(1)
где ψ – угол рыскания летательного аппарата (ЛА);
θ – угол тангажа ЛА;
γ – угол крена ЛА;
, 
, 
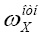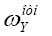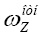– проекции угловой скорости связанной с ЛА системы координат OXYZ относительно географической системы координат.
2 Моделирование алгоритма ориентации в среде Matlab
Схема моделирования уравнений (1) в пакете Simulink программы Matlab приведена в [1]. Однако в указанной схеме отсутствуют средства оценки точности моделирования. Указанный недостаток устраняется при введении в схему разности сигналов с блоков задания углов поворота ЛА (psi, theta, gamma) и сигналов на выходах алгоритма ориентации. Схема моделирования представлена на рис. 1.
В представленной схеме численное дифференцирование выполняется в блоке пересчета углов Эйлера-Крылова в проекции относительной угловой скорости на оси связанного с ЛА трехгранника. Для оценки влияния процедуры численного дифференцирования, соответствующие блоки были исключены из схемы и введены аналитические выражения для производных:
где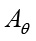 
, 
, 
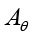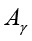– амплитудные значения углов рыскания, тангажа и крена ЛА;
, 
, 
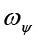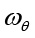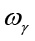– угловые частоты изменения углов рыскания, тангажа и крена ЛА;
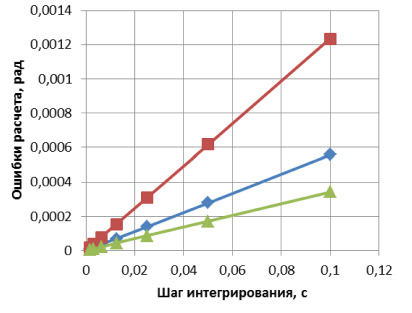
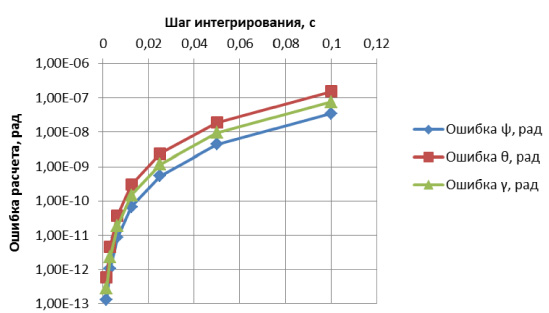
Моделирование выполнялось на интервале времени 50 с, с фиксированным шагом интегрирования, который варьировался в ходе вычислительного эксперимента. Результаты моделирования представлены на рис. 2.
Как видно из полученных зависимостей, исключение блоков дифференцирования позволило уменьшить ошибку восстановления углов поворота ЛА на четыре порядка при максимальном шаге интегрирования 0,1 с. Полученный результат дает основание для утверждения того, что операция численного дифференцирования вносит наибольший вклад в погрешность моделирования алгоритма БСО.
; 
; 
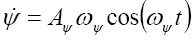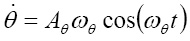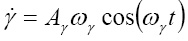, (2)
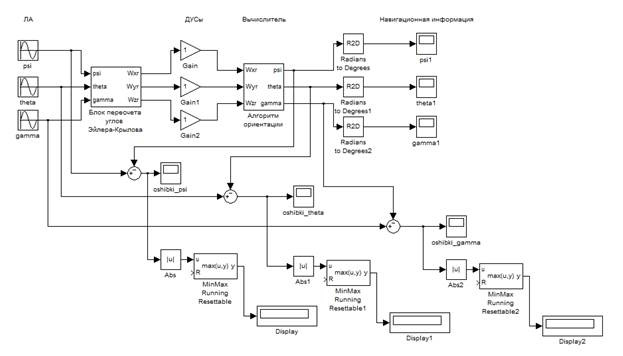
Рис. 1. Схема моделирования алгоритма ориентации в MATLAB
а) б)
Рис. 2. Графики ошибки моделирования алгоритма ориентации в Matlab:
а) при наличии блоков дифференцирования;
б) при отсутствии блоков дифференцирования
3 Моделирование алгоритма ориентации в среде Mathcad
Одним из достоинств системы Mathcad является графический ввод выражений, что заметно уменьшает время, затрачиваемое на формирование математической модели исследуемого объекта. Данная особенность позволяет использовать выражения (1) в привычном виде, без дополнительных операций, связанных с адаптацией выражений к синтаксису среды моделирования.
В среде Mathcad при дифференцировании функций, заданных в аналитическом виде, автоматически задействуется символьный процессор, что позволяет избежать ошибок численного дифференцирования. Для оценки влияния процедуры дифференцирования в среде Mathcad была сформирована процедура моделирования алгоритма БСО по уравнениям (1).
Моделирование выполнялось на отрезке времени 10 с., с шагом 0,01 с. Точность решения, определяемая системными переменными TOL и CTOL, была установлена по умолчанию (TOL = CTOL = 0,001). Для решения системы уравнений (2) была применена встроенная в Mathcad функция rkfixed решения системы дифференциальных уравнений методом Рунге – Кутта с фиксированным шагом.
По результатам моделирования (рис. 3) было установлено, что наличие операторов дифференцирования не приводит к увеличению ошибки моделирования алгоритма ориентации БСО. Данное обстоятельство подтверждает тот факт, что для функций, заданных аналитически, вычисления в среде Mathcad выполняются в символьном виде, не оказывая влияние на точность получаемых результатов.
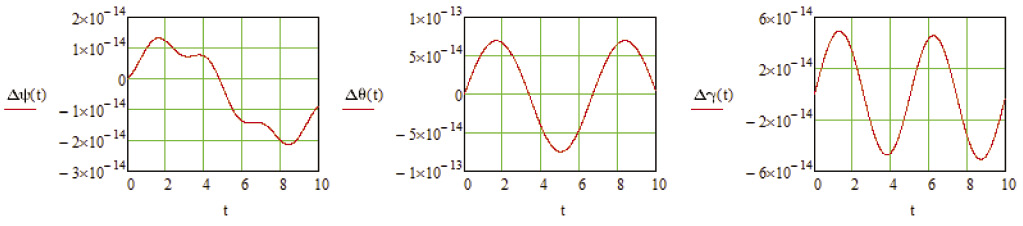
Рис. 3. Графики ошибок моделирования алгоритма ориентации в программе Mathcad
Таким образом, точность восстановления углов ориентации ЛА в среде моделирования Mathcad соответствует точности восстановления при моделировании алгоритма ориентации в среде Matlab/Simulink в случае исключения блоков численного дифференцирования, т.е. при вычислении производной в символьном виде.
Заключение
Прямое численное дифференцирование приводит к погрешностям в любой вычислительной среде, в этой связи вычисление производных для функций, заданных в аналитическом виде, целесообразнее выполнять в символьном виде.
Южно-Уральский государственный университет https://susu.ru