В процессе решения задач построения диагностических правил возникают вопросы анализа репрезентативности обучающих выборок, представляющих диагностические классы. В большинстве медицинских исследований, касающихся онкологических заболеваний желудка, в конкретном регионе весьма проблематично сформировать обучающие выборки, отвечающие принципам доказательной медицины.
Поскольку для анализа различий требуется достаточный объем статистического материала с точки зрения доказательной медицины [1] , который зачастую отсутствует, то на этапе оценки коэффициента уверенности в адекватности используемых выборок (Кув) предлагается поступить следующим образом, опираясь на методологию системного анализа.
1. Оценить законы распределения представленных рядов двумя способами. Во-первых, путем сравнения ассиметрии и экцесса со вспомогательными коэффициентами по классическим статистическим методам. На данном этапе исследуются законы распределения анализируемых и латентных показателей с помощью вычисления соответствующих значений ассиметрий и эксцессов. Если удвоенные значения ассиметрии и экцесса анализируемой выборки меньше определенных коэффициентов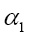 
и 
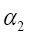(соответственно), то распределение считается нормальным. Коэффициенты вычисляются по следующим формулам [2]:
(1),
(2)
При недостаточности объема выборок предлагается применить метод приведенных значений, предложенный Уразбахтиным И.Г. [3], сущность которого заключается в определении индикаторов (оценки среднеквадратичного отклонения и математического ожидания) выборки после нормирования исходных данных в диапазон [0+e,1-e] (e=1/N, где N – количество элементов исходного множества) путем линейного преобразования и применения специальных таблиц (функций), ставящих соответствие между законами распределения и полученной величиной указанного отношения. Приведение в указанный диапазон с учетом статистической мощности выборки n осуществляем по формуле (3) следующего линейного преобразования для некоторого вектора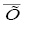 
в вектор 
:
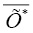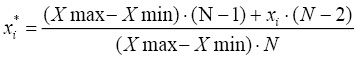(3),
где Xmax, Xmin – максимальное и минимальное значения элементов вектора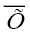 
.
Затем, для Х* вычисляется математическое ожидание и дисперсия и, согласно приведенному ниже рисунку 1, оценивается принадлежность к определенному распределению.
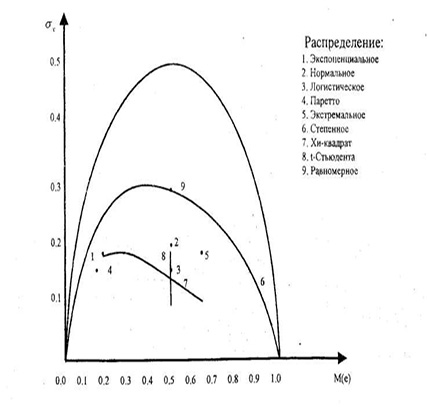
Рисунок 1. Нормированные распределения.
2. Для рядов, для которых идентифицирована принадлежность к нормальному распределению определяется доверительный интервал на уровне статистической значимости Р<0,05. Для других распределений в качестве доверительного интервала используется универсальное правило «2 сигм». (При малом объеме выборок – менее 20 элементов обучающего множества - согласно [4] рекомендуется применять правило «2.5*сигм»).
3. Определяются значения следующих трех показателей по формулам:
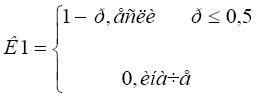
(4),
где p – вероятность ошибки первого рода.
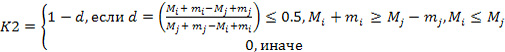(5),
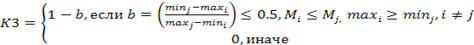(6).
Где индексы – «номера» сравниваемых классов состояний.
4. По вычисленным значениям указанных показателей вычисляется коэффициент уверенности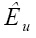 
(лежит в интервале [0,1]):
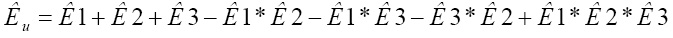(7).
По полученным значениям делается заключение о том, что уверенность в статистически значимой различимости множеств для решения классификационных задач лежит в интервале: 