Современное машиностроение требует непрерывного повышения технического уровня механических трансмиссий. При необходимости преобразования вращательного движения входного в поступательное движение выходного звена в составе трансмиссий находят широкое применение винтовые механизмы (передачи винт-гайка), различающиеся как конструктивным исполнением, технико-эксплуатационными характеристиками, так и принципом передачи движения.
Конструкция передачи винт-гайка скольжения отличается значительными потерями на трение, низким коэффициентом полезного действия (КПД менее 40 %), высокой изнашиваемостью, большим мертвым ходом, не плавностью при малых скоростях движения и ограниченной нагрузочной способностью при обеспечении точного и плавного перемещения. Разделение винтовых поверхностей винта и гайки нагнетаемой между ними под давлением рабочей жидкостью в гидростатических передачах способствует повышению стоимости передачи, снижению ряда эксплуатационных характеристик, увеличению сложности системы в целом, необходимости компенсации колебаний температуры и т.д.
Это потребовало создания несоосных винтовых механизмов (НВМ), отвечающих сумме требований, предъявляемых к кинематическим и силовым механизмам [1]. НВМ, в том числе роликовые винтовые передачи (РВП), находят все большее применение в механической части точных приводов в различных отраслях промышленности. РВП по сравнению с шариковыми винтовыми передачами (ШВП) имеют целый ряд преимуществ: по редукции (в 100 раз), грузоподъемности (в 4 – 5 раз), долговечности, компактности, жесткости (в 1,5 – 2 раза), точности (до 0,002 мм), приведенному моменту инерции (ниже в 2 – 10 раз), расширению диапазона частот вращения центрального винта (в 3 – 5 раз), линейной скорости перемещения гайки (в 2 – 3 раза) [2].
НВМ включают в себя большое число как схемных, так и конструктивных разновидностей, построенных на базе двух основных решений – внутреннего или внешнего сопряжения несоосных друг другу резьб винта и гайки. При эксплуатации НВМ в контакте резьб на ведомое звено со стороны ведущего звена действует не только силы давления, но и сила трения. В отличие от других винтовых передач в НВМ вращение винта преобразуется в поступательное движение гайки за счет одновременного действия сил давления и фрикционной силы в контакте.
В общем случае передача является фрикционной. Трение в контакте резьб смешанное, качение со скольжением. При одном и том же коэффициенте и силе трения ее плечо, а, следовательно, и момент трения в передаче будут значительно меньше, чем у обычной передачи винт-гайка скольжения. КПД при углах подъема резьбы 4 – 5° может достигать 80 – 93 %. Благодаря несоосности и одновременному вращению сопряженных винтовых поверхностей, направление относительной скорости скольжения резьб друг по другу, а, следовательно, и силы трения значительно отклоняется от направлений окружных скоростей вращения винта и гайки. Вектор силы трения в НВМ может менять свое направление в плоскости, перпендикулярной общей нормали к сопрягаемым поверхностям, в диапазоне угла 360°.
Винт является наиболее ответственной и сложной деталью любой винтовой передачи вследствие большой протяженности его несущей винтовой поверхности и малой жесткости. Винты НВМ выполняют цельными и составными, с одним, двумя и более участками резьбы, малого, среднего и большого диаметров; одно и многозаходные.
Для всех сопрягаемых деталей НВМ наиболее жесткие требования предъявляются к несущей винтовой поверхности по точности шага профиля и среднего диаметра, точности диаметральных размеров. Так как длина винта, и даже длина его резьбовой поверхности, во много раз превосходит диаметр, тело винта обладает недостаточной жесткостью.
При оценке качества винтовых механизмов уделяется большое внимание быстродействию и точности отработки заданного закона движения, глубине регулирования и возможности плавного изменения скорости выходного звена, высокой плавности движения, особенно на малых скоростях, минимальной величине кинематической погрешности. Все приводы с передачей винт-гайка должны обеспечивать минимальные энергетические потери, высокий коэффициент полезного действия, иметь малые массу и габаритные размеры, высокую надежность, а также отличаться технологичностью изготовления, ремонта и эксплуатации.
Все винтовые механизмы обычно подразделяют на кинематические, используемые в малонагруженных приводах приборов и систем управления, и силовые, работающие при значительных нагрузках на ходовой винт. К кинематическим передачам винт-гайка предъявляются высокие требования по точности, а к силовым – по прочности и износостойкости.
Развитие современной техники потребовало создания таких винтовых механизмов, которые удовлетворяют всему комплексу требований, предъявляемых как к кинематическим, так и к силовым механизмам. Детали несоосных винтовых механизмов в процессе эксплуатации подвергаются нестационарному повторно-переменному нагружению и выходят из строя в результате усталостного разрушения. С целью повышения долговечности сопрягаемые детали НВМ подвергают упрочняющей обработке. Для технологического обеспечения долговечности и качества передачи необходима информация о напряженном состоянии деталей, формирующемся в процессе эксплуатации НВМ [1, 6].
Расчет экстремальных напряжений ходового винта от деформаций изгиба, кручения, растяжения (сжатия), среза.
Данная работа посвящена решению задачи по определению экстремальных и расчетных напряжений в любой точке детали НВМ при эксплуатации [7] и вклад каждого из видов деформаций на величину эквивалентных напряжений. Напряженное состояние ходового винта формируется в результате взаимодействия сопрягаемых поверхностей винта и гайки (для простого НВМ) или винта и роликов (для РВП). В связи с фрикционным характером передачи движения, при рассмотрении силового взаимодействия контактирующих поверхностей учитывалось суммарное влияние сил давления и трения. При определении главных напряжений выделяли внутри детали три области [5, 8, 12].
В каждой области результирующие напряжения являются некоторой суммой нормальных и касательных напряжений от всех рассматриваемых видов деформаций (деформаций тела винта, витка и контактных деформаций). Зная нормальные и касательные составляющие напряжений по граням элементарного объема легко определить экстремальные и расчетные напряжения для любой точки выше рассмотренных областей [3, 4].
Задача определения напряженного состояния сводится к расчету главных (экстремальных) напряжений от всех действующих силовых факторов в любой точке детали в произвольный момент времени [9]. Данные о значениях экстремальных напряжений в локальной области несущей детали НВМ в тот или иной момент времени являются основой расчета параметров спектра нагружения и глубины наиболее нагруженного несущего слоя. Сведения о спектре нагружения несущей поверхности дают возможность прогнозировать ее долговечность. Знание глубины несущего слоя позволяет предъявить научно обоснованные требования к величине, знаку и градиенту изменения технологических остаточных напряжений. Это создает предпосылки выбора рационального технологического маршрута и режимов обработки несущей поверхности [10].
При расчете деталей несоосных винтовых механизмов наибольший интерес вызывает напряженное состояние наиболее ответственной детали передачи – ходового винта. В случае равномерного распределения рабочей нагрузки между роликами передачи, поля напряжений, сформированные в винте под действием сил от каждого из роликов, компенсируют друг друга, а величины главных напряжений зависят только от величины осевой составляющей нагрузки и диаметра винта. Однако в реальной передаче вследствие погрешностей сборки и изготовления отдельных звеньев, нагрузка между роликами распределяется неравномерно. В работе предпринята попытка оценить степень влияния каждого из вида деформации на величину главных напряжений в ходовом винте [11].
При расчете главных напряжений ходовой винт допустимо моделировать брусом круглого сечения с закрепленными в опорах концами. Известно, что подавляющая доля нагрузки воспринимается первыми витками резьбы, находящимися в контакте с сопрягаемой деталью. Так как расстояние между соседними витками резьбы винта, воспринимающими нагрузку, составляет 0,4…2,5 мм, что много меньше длины винта, силы, действующие на виток резьбы, считаются лежащими в одном поперечном сечении. Таким образом, при проведении расчетов вся нагрузка считается сосредоточенной в одном поперечном сечении. Рассматривается плоское напряженное состояние винта. Определяются главные напряжения, формирующиеся в результате взаимодействия полей напряжений изгиба, кручения, растяжения, сжатия и сдвига [13, 14].
В результате аналитического решения задачи получены выражения для определения главных напряжений в любой точке винта. Предлагаемые зависимости при знании закона изменения во времени координат точки приложения нагрузки, позволяют оценить динамику изменения экстремальных напряжений в процессе эксплуатации, определить параметры спектра нагружения, произвести расчет винта на долговечность.
Численный расчет по предлагаемой методике проводился для ходового винта РВП с 9-ю роликами, имеющего средний диаметр резьбы винта d = 25 мм, угол профиля резьбы 2a=90°, угол подъема винтовой линии l=7,256°, шаг S= 2 мм, ход p=10 мм, количество заходов резьбы – 5. Построены графики зависимости суммарных эквивалентных напряжений от напряжений витка, винта и контактных напряжений при двух значениях угла профиля резьбы (рис. 1, 2).
Эквивалентные напряжения определяли в наиболее характерной области 2, где действуют все виды напряжений – напряжения от деформаций витка, винта и контактных деформаций.
Выводы
Расчет показал, что (рис. 1, 2):
1. Наибольший вклад в эквивалентные суммарные напряжения вносят контактные напряжения (до 80 %), наименьшие – напряжения витка (до 3 %);
2. Напряжения витка и тела винта составляют от 3 % до 35 % от эквивалентных суммарных напряжений в зависимости от величины угла профиля резьбы.
Следовательно, для данного механизма напряжениями от деформаций витка можно пренебречь. При изменении некоторых параметров передачи, например, угла профиля резьбы, напряжения витка и тела винта достигают 35 % от суммарных эквивалентных напряжений. В этом случае необходимо учитывать все виды напряжений.
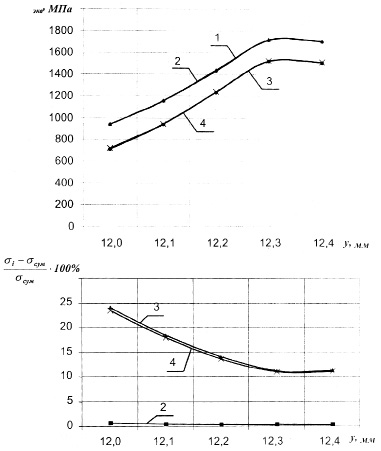
Рис. 1. Значения эквивалентных напряжений при l=7,256°, a=45°, f=0,1: 1 – с учетом всех деформаций; 2 – без учета деформаций витка; 3 – без учета деформаций тела винта; 4 – без учета деформаций витка и тела винта
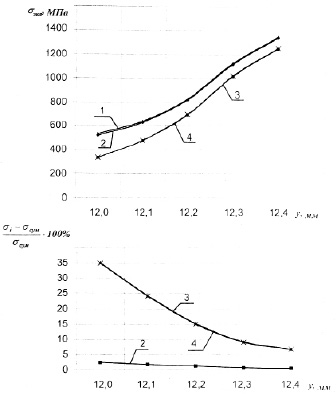
Рис 2. Значения эквивалентных напряжений при l=7,256°, a=30°, f=0,1: 1 – с учетом всех деформаций; 2 – без учета деформаций витка; 3 – без учета деформаций тела винта; 4 – без учета деформаций витка и тела винта



