Аппарат линейной алгебры может быть использован для построения микроэкономических моделей, а именно отыскание собственных чисел и собственных векторов квадратной матрицы.
При исследовании различных экономических ситуаций возникает необходимость рассматривать матрицу обмена и находить ее собственные векторы.
Рассмотрим задачу о равновесии цен в простой модели обмена.
Пусть имеется система из n отраслей производства, каждая из которых выпускает продукцию одного вида. Примем за единицу объем продукции каждой отрасли в рассматриваемом периоде. Обмен продукцией происходит только внутри системы (экономика замкнута) и известна матрица А:
(1)
где αij – доля продукции j-й отрасли, которая поступает в i-ю отрасль.
Ясно, что для матрицы А выполнены два условия:
αij ≥ 0, I = 1,2,…n;
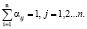
Второе условие вызвано тем, что вся продукция j-ой отрасли предназначена для обмена внутри системы. Матрица (1), для которой выполнены условия 1 и 2, называется матрицей обмена. Требуется установить такие цены на продукцию каждой отрасли, при которых вся система находится в равновесии, т.е. ни одна отрасль не обогащается за счёт другой.
Пусть хi – цена одной единицы продукции i-й отрасли, а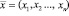 
– вектор цен. Тогда расход i-й отрасли, т.е. стоимость всей закупаемой ею продукции, таков: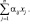 
Чтобы отрасль могла развиваться, её расход не должен превышать дохода, который равен стоимости произведённой ею продукции, т.е. xi:
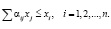(2)
Если искомые равновесные цены существуют, то система неравенств (2) выполняется для них как система равенств: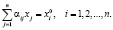 
Таким образом, задача свелась к следующему:
1. выяснить, является ли число λ=1 собственным числом матрицы обмена А;
2. если да, то найти соответствующий этому собственному числу полуположительный собственный вектор матрицы А.
Для того чтобы число λ=1 было собственным числом матрицы обмена А, необходимо и достаточно, чтобы выполнялось равенство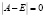 
.
Итак, число 1 является собственным числом матрицы обмена и для отыскания соответствующего ему собственного вектора следует найти полуположительное решение однородной системы (A – E)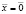 
. Найденный полуположительный вектор 
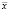является искомым вектором равновесных цен.
Рассмотрим пример: экономическая система состоит из трёх отраслей производства, каждая из которых выпускает один вид продукции. Обмен внутри системы происходит в соответствии с данной матрицей обмена
.
Найдем вектор равновесных цен. Составим однородную систему линейных уровнений (А-Е)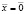 
:
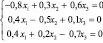
Решив её, получим:
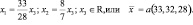
Полагая а > 0, находим равновесные цены на продукцию каждой отрасли: х1=33а; х2=32а; х3=28а, где а можно трактовать как множитель, связанный с денежной единицей.
Другая экономическая модель, где решается математическая задача того же вида, – это модель международной торговли. Рассмотрим систему из п стран, торгующих только друг с другом (т.е. система замкнута). Известна матрица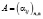 
, где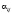 
– доля средств j-й страны, затрачиваемая на импорт из i-й страны. Матрица А является матрицей обмена (1), т.е. 
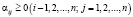и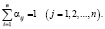 
Требуется найти первоначальное распределение средств между странами, обеспечивающее равновесие всей системы, т.е. такое положение, при котором в каждой стране после каждого цикла обмена остаётся столько же средств, сколько было до обмена.
Пусть хi – количество средств i-й страны, т.е. вектор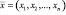 
описывает искомое распределение средств. Ясно, что надо найти вектор 
, удовлетворяющий условиям
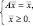
Ранее было показано, что число 1 есть собственное число матрицы обмена А и что существует полуположительный собственный вектор 
матрицы А, соответствующий этому собственному числу. Вектор 
и является искомым первоначальным распределением средств. Система при этом будет находиться в равновесии, т.е. расход каждой страны в каждом цикле обмена совпадает с её доходом от экспорта и не изменяется от цикла к циклу.