Среди множества задач оптимизации особую роль в силу своей практической значимости играют задачи линейного программирования. Одной из распространенных задач является задача на оптимальное использование ресурсов. Рассмотрим задачу на оптимальный выпуск мороженного и дадим экономический анализ решения на устойчивость.
Фирма выпускает два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы даны в таблице.
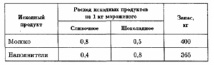
Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 р., шоколадного – 14 р. Какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?
Целевая функция будет иметь вид
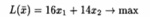
при ограничениях:
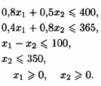
Решив задачу графически находим оптимальное решение: xопт=(312,5;300) Фирма должна выпускать в сутки 312,5 кг сливочного мороженного и 300 кг шоколадного.
Проведем экономический анализ рассмотренной выше задачи:
Рассмотрим увеличение ресурса по молоку. Получим предельно допустимый суточный запас молока: = 432,1 кг. Предельно допустимый суточный запас наполнителей можно увеличивать до значения 392,5 кг. Не изменяя оптимальное решение правую часть ограничения можно уменьшать до величины 312,5–300=12,5 кг.
При неизменном оптимальном решении разница в покупательском спросе на сливочное и шоколадное мороженое может изменяться в диапазоне от 12,5 до 500 кг.



