Детерминистические фрактальные решетки являются представителями фракталов с конечным ветвлением и, как правило, построены из затравки в виде определенного фрагмента 2D-решетки [1]. Геометрическим генератором фрактальных решеток может быть фрагмент 2D дважды периодических полигонных R{Pg}im-структур, в частности, тетрагонных R{4}im-структур, соответствующих 2D-сетке 4444 или ее производным [1]. При этом предполагается, что в вершинах тетрагона могут располагаться атомы, комплексные частицы – молекулы, кластеры.
Процедура формирования генератора G = LN{4}, i, k из квадратного фрагмента тетрагонной R{4}im-структуры определяется законом транскрипции, а процедура получения самоподобных фрактальных решеточных n-структур FN{4},i,k{2-} – итерационным законом, где N – количество тетрагонов {4} в квадратном фрагменте 2D-пространства со стороной b; i – характеристика «ядра» двумерной тетрагонной структуры, которая определяла способ его ветвления (посредством вершин iv или сторон ir тетрагона); k = b-1 – коэффициент самоподобия генерируемой фрактальной FN{4}ik-структуры; {2-} – классификационный параметр, указывающий топологическую размерность инициального объекта (плоскости) и тенденцию изменения размерности при переходе к генератору, n – целочисленный индекс, характеризующий количество применяемых итераций [2-5].
Фрактальная размерность Dim решетки в соответствии с [1] может быть определена из соотношения
Dim = lnN (lnb)–1,
где N – число тетрагонов в генераторе, b – сторона генератора (в отн. ед.).
Тогда, если (b2 – N) – число лакун в квадратном генераторе, имеем следующее соотношение
Dimlac = ln(b2 – N) (lnb)–1 ,
где Dimlac – лакунарная размерность фрактальной решетки, характеризующая возможное дополнение данной фрактальной решетки до 2D тетрагонной R{4}im-структуры. Все FN{4},i,k-структуры отличаются по своим лакунарным спектральным характеристикам, которые можно считать диагностическими [6-15]. Отметим, что каждая из FN{4},i,k -структур формально может быть первым членом гомологического ряда соответствующих структур (рис. 1). Полученные с помощью итерационного модулярного дизайна на тригонной сетке фрактальные решетки с FN{3},i,k-структурами также соотносятся с гомологической серией фрактальных структур вида F(6+2n){3}, I, 1/(3(2+n))1/2 и F(3+3n){3}, I, 1/(2+n) и классической треугольной косынкой Серпинского F3{3},3(r),1/3 [1] (рис. 2).
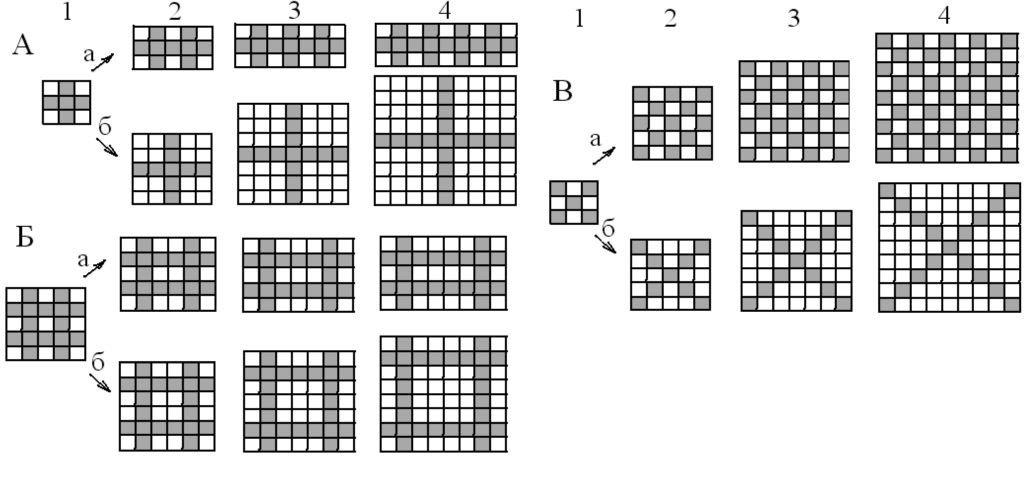
Рис. 1. Изображения первых четырех членов трех пар гомологических рядов детерминистических решеток с генераторами L(1+4n) {4},i, [3(1+2n)]1/2 (А-а), L(1+2n+2n2) {4},i, (1+2n) (А-б), L(14+2n) {4},i, [5(4+n)]1/2 (Б-а), L(12+4n) {4},i, (4+n)] (Б-б), L(1+4n) {4},i, (1+2n) (В-а) и L(1+4n) {4},i, (1+2n) (В-б)
Фрактальные размерности тетрагонных FN{4},i,k и тригонных FN{3},i,k -структур закономерно изменяются с увеличением порядкового номера n в соответствующем гомологическом ряду генераторов внутри интервала значений Dim [1, 2] (рис. 3). Аналогичные закономерности наблюдаются и для лакунарных размерностей указанных структур. Значения локальной и лакунарной размерностей для каждой фрактальной структуры могут быть использованы при определении квазиупорядоченного сайт-распределения определенных фаз по поверхности композиционного покрытия и конфигурационных характеристик межфазных границ. На основе этих данных возможна оценка поверхностной доли твердого смазочного компонента и расчет трибологических свойств покрытия в соответствии с синергической моделью [16].
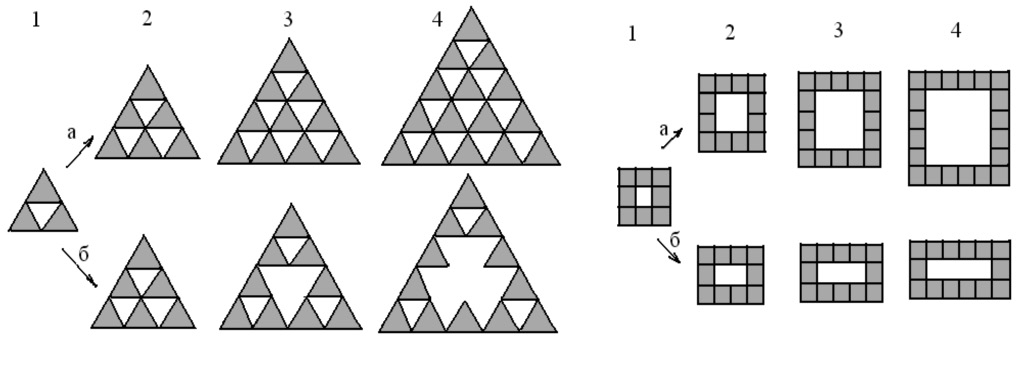
Рис. 2. Изображения первых четырех членов гомологических рядов салфеток Серпинского с генераторами L(4+4n){4}, i, 1/(2+n) (а), L(3+3n){4}, i, 1/(2+n) (б) (слева) и ковров Серпинского с генераторами L(6+2n){3}, i, 1/(3(2+n))1/2 (а), L(4+4n){3}, i, 1/(2+n) (б)
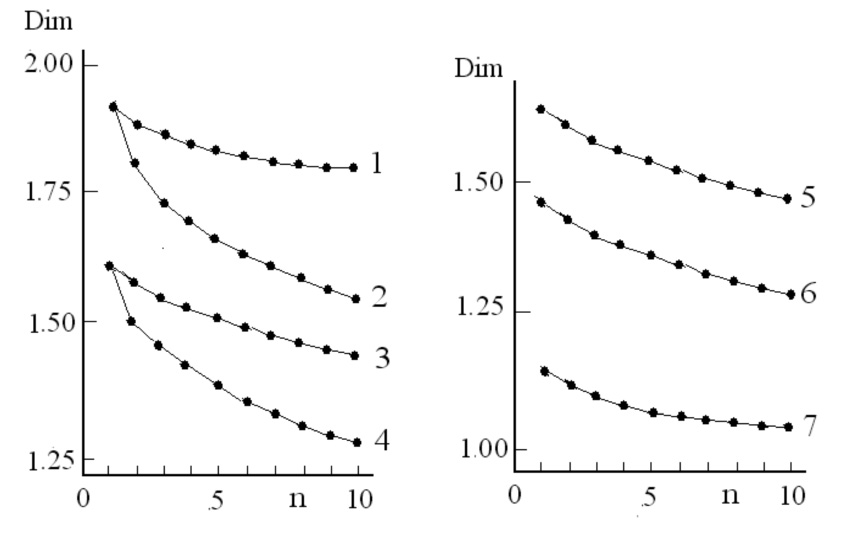
Рис. 3. Изменение размерности фрактальных структур вида FN{4}ik{2-} от порядкового номера n в гомологических рядах генераторов салфеток Серпинского L(6+2n){3}, i, 1/(3(2+n))1/2 (1) и L(4+4n){3}, i, 1/(2+n) (2), ковров Серпинского L(4+4n){4}, i, 1/(2+n) (3) и L(3+3n){4}, i, 1/(2+n) (4), решеток L(4+2n){3}, i, 1/(2+n) (5), L(1+4n){3}, i, 1/(3(2+n) (6) и L(4+8n){3}, i, 1/(2+4n) (7)
Отметим, что приведенные выше примеры рядов генераторов фрактальных структур вида FN{4},i,k могут быть существенно дополнены множеством рядов генераторов, отражающих результат клеточной аппроксимации последовательных стадий «роста» различных линий 3-го и 4-го порядка, а также трансцендентных линий, в том числе спиралей и циклоидальных кривых.
Таким образом, в 2D-пространстве могут быть сформированы фрактальные структуры вида FN{4},i,k{2-}. Данные фрактальные структуры характеризуются размерностями практически во всем диапазоне значений в интервале от 1 до 2 и могут быть использованы для интерпретации результатов исследований трибологических свойств поверхности композиционных материалов и покрытий [16-19].
Работа выполнена при финансовой поддержке Министерства образования и науки РФ, соглашение № 14.U01.21.1078.



