Непрерывное весовое дозирование сыпучих материалов широко используется в различных отраслях промышленности [1]. Основной метрологической характеристикой дозаторов является точность дозирования. Высокая точность дозирования особенно важна при организации процесса смешивания, поскольку именно от точности дозирования, во многом, зависит качество готовой смеси [2, 3]. Для повышения точности дозирования ранее [4] была предложена двухстадийная технология дозирования и устройство для ее реализации [5]. Сущность данной технологии заключается в том, что на первой стадии формируются отдельные порции определенного веса, а на второй стадии эти порции преобразуются в непрерывный поток. Преобразование отдельных порций в непрерывный поток возможно с использованием наклонного вибрирующего лотка с прямоугольным поперечным сечением. Результаты эксепериментов показали, что в процессе преобразования порций изменяется их форма и происходит перемещение вдоль лотка. Характерный пример движения отдельной порции показан на рис. 1.
Для расчета процесса двухстадийного дозирования, в частности, необходимо знать по каким законам происходит изменение формы порции сыпучего материала под действием вибрации. Для решения данной проблемы была проведена видеосъемка движения частиц в горизонтальном вибрирующем лотке, характерные результаты которой показаны на рис. 2.

Рис. 1. Разложение по кадрам видеоизображения процесса движения порции сыпучего материала по наклонному вибрирующему лотку
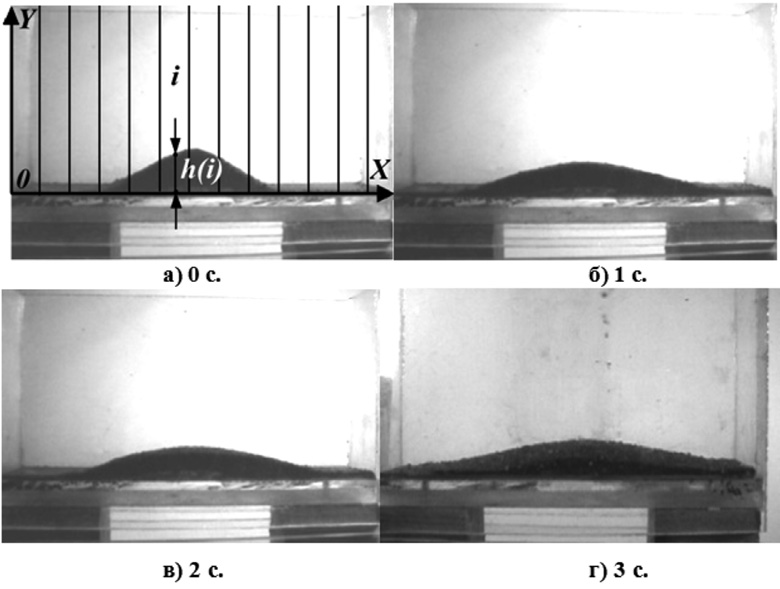
Рис. 2. Изменение формы открытой поверхности порции сыпучего материала
Для построения математической модели процесса необходимы экспериментальные данные об изменении формы порции материала под действием вибрации. Для сокращения временных затрат на экспериментальные исследования было разработано программное обеспечение (ПО), суть которого заключается в следующем:
1. Цифровое изображение лотка делится на равные участки по его длине (рис. 2а). Осуществляется вертикальное сканирование изображения, в процессе которого определяется высота материала h(i) в каждом i-м разбиении.
2. Рассчитывается объем материала на каждом участке V(i)=S h(i) Δl, где S – ширина лотка, Δl – длина участка и определяется координата центра тяжести hц.т.(i)=h(i)/2. Учитывая, что мы задаемся очень малой величиной Δl, ошибка в определении hц.т.(i) минимальная.
3. Определяется масса m(i)=ρV(i), где ρ – плотность насыпи вещества.
4. Определяется значение потенциальной энергии сыпучего вещества i-го участка по следующему соотношению W(i)=m(i)g h(i). Окончательно, потенциальная энергия сложной фигуры находится, как сумма потенциальных энергий элементарных фигур.
Проверкой нахождения центра тяжести фигуры из сыпучего материала может служить идеализированный пример, когда сечение порции сыпучего материала представляет собой равнобедренный треугольник. Как известно, центр тяжести равнобедренного треугольника находится на расстоянии одной трети длины высоты, считая от основания.
Работа программы для реального примера показана на рис. 3.
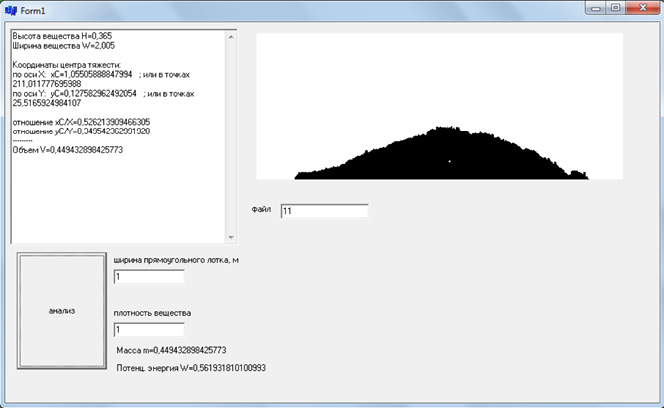
Рис. 3. Определение центра тяжести порции сыпучего материала
Теоретические и экспериментальные данные практически полностью совпадают. Полученная математическая модель позволяет находить центр тяжести порции сыпучего материала и изменение потенциальной энергии порции. Это существенно снижает трудоемкость при проектировании двухстадийных дозаторов, в которых в качестве преобразователя отдельных порций в непрерывный поток, используется наклонный лоток с прямоугольным поперечным сечением, совершающий вертикальные колебания.



