В 1202 году в «Книге Абака» средневекового математика Леонардо Пизанского, известного как Фибоначчи, появляется особая последовательность чисел – 1, 1, 2, 3, 5, 8, 13, 21 и т.д., названная в последствии числами Фибоначчи [1]. Уникальность этого ряда заключается в том, что отношение каждого последующего числа к предыдущему – есть величина постоянная. Лука Пачоли, современник и друг Леонарда да Винчи, называл это отношение «божественной пропорцией», а в 1835 году Мартином Омом был введен в обиход термин «золотое сечение». Правило «золотого сечения» использовалось во все времена в искусстве, кинематографе, строительстве, механике.
Авторами настоящей статьи предпринята попытка применения правила «золотого сечения» к разработке форм бойков ударных механизмов. В частности, предлагается боек, состоящий из двух ступеней цилиндрической формы (рисунок 1), диаметры и длины которых соотносятся согласно правилу «золотого сечения» и определяются формулами
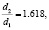
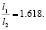 (1)
(1)
Для обоснования применения «золотого сечения» к созданию бойков решена задача об определении ударного импульса, генерируемого в полубесконечном стержне, при ударе по нему бойком цилиндрической формы (рис. 1). В результате проведения расчетов установлено, что применение правила «золотого сечения», для создания бойков целесообразно лишь при наличии конструктивных ограничений на размеры корпусов ударных механизмов.
Одним из недостатков цилиндрических бойков является прямоугольная форма импульса (рис. 1), генерируемого при ударе по волноводу.
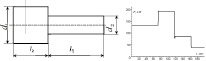
Рис. 1. Двухступенчатый цилиндрический боек, построенный по правилу «золотого сечения», и генерируемый им импульс
Этот недостаток в двухступенчатых бойках может быть устранен путем выполнения ударной части бойка в форме усеченного конуса (рисунок 2). При таком условии генерируемый цилиндроконическим бойком ударный импульс будет иметь экспоненциальную форму с нарастающей амплитудой [2].

Рис. 2. Цилиндроконический боек
Для обеспечения устойчивого положения такого бойка в корпусе ударного механизма необходимо, чтобы размеры бойка выбирались в соответствии с соотношением [3]
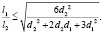 (2)
(2)
Практический анализ формулы (2) показал, что создание цилиндроконических бойков, в которых длины степеней задаются исходя из правила «золотого сечения» 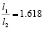 , обеспечит расположение центра масс в цилиндрической части, тем самым придавая бойку устойчивое положение в корпусе механизма
, обеспечит расположение центра масс в цилиндрической части, тем самым придавая бойку устойчивое положение в корпусе механизма



