В работе [1] профессором В.В. Добровольским был введен параметр mД, означающий число степеней свободы всего механизма, и записана так называемая универсальная формула подвижности механизмов в виде
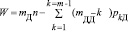 , (1)
, (1)
где W – число степеней свободы механизма, n – число подвижных звеньев, kД – род кинематических пар по В.В. Добровольскому. В зависимости от параметра mД, могущего принимать значения 2, 3, 4, 5 или 6, все механизмы В.В. Добровольским были разделены на пять родов. Однако такая классификация в теории механизмов не «прижилась».
Позже, в работе [2] профессор И.И. Артоболевский предложил ввести понятие числа общих наложенных на весь исследуемый механизм связей m. Этот параметр связывается с mД выражением m=6–mД. Учитывая это, формула подвижности (1) была приведена И.И. Артоболевским к следующему виду
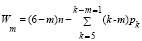 , (2)
, (2)
где Wm определяет подвижность механизма. В зависимости от значений, принимаемых параметром m в формуле (2), И.И. Артоболевский выделил пять семейств механизмов: нулевое (m=0), первое (m=1), второе (m=2), третье (m=3) и четвертое (m=4) [2].
Вводя в формулу (2) соответствующие значения для m, получим структурные формулы подвижности каждого из семейств (3) – (7) механизмов, определяющие зависимости между числом звеньев и кинематических пар
нулевое (m=0) 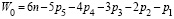 , (3)
, (3)
первое (m=1) 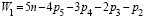 , (4)
, (4)
второе (m=2) 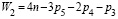 , (5)
, (5)
третье (m=3) 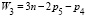 , (6)
, (6)
четвертое (m=4) 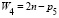 . (7)
. (7)
На рисунке приведены примеры механизмов всех пяти семейств. Подвижность каждого из механизмов может быть сосчитана по структурной формуле соответствующего семейства.
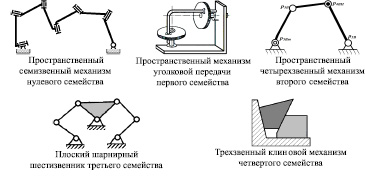
Механизмы нулевого, первого, второго, третьего и четвертого семейства
Число общих наложенных на механизм связей однозначно определяет его структурную формулу и в зависимости от этого числа существуют пять семейств отличающихся друг от друга механических систем.
В работе [3] было предложено внутри семейств в соответствии с составом используемых кинематических пар различных классов выделять отличающиеся друг от друга подсемейства. В нулевом семействе таких подсемейств оказалось 31, в первом 15, во втором 7, в третьем 3 и в четвертом 1. Обязательным условием для подсемейств является такое, что числа кинематических пар в их уравнениях не могут принимать нулевых значений.
Из изложенного следует, что изучение полного многообразия возможных к применению механизмов требует систематического их разделения на семейства и подсемейства в зависимости от числа общих наложенных на механизмы условий связи и классов используемых в них кинематических пар.



