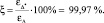Подшипники являются одним из важных деталей роликовых коньков и несут почти все нагрузки, которые создаются при катании. С учётом относительно низкой скорости и нагрузки, а также малую информированность потребителя об основных параметрах качества подшипников многие производители роликовых коньков используют в своей продукции подшипники сомнительного качества, что позволяет им снижать себестоимость.
Скоростные характеристики подшипников для роликовых коньков имеют второстепенное значение, главное в подшипниках для роликовых коньков это надёжность, которая в первую очередь обеспечивается:
- качеством материала (специальные стали и сплавы, для тел качения и колец, специальные смазки и материалы уплотнений);
- качеством сборки (даже из качественных комплектующих без соответствующего оборудования и опыта невозможно собрать качественное изделие);
- качеством защиты рабочих поверхностей от внешнего воздействия.
Так в роликовых коньках используются подшипники типоразмера 608, выпускаются открытого и закрытого (предварительно смазанные и не требующие обслуживания) типа.
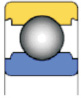
608 (открытого типа)
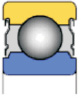
608ZZ (закрытый металлическими защитными шайбами)
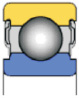
608EE (закрытый уплотнениями)
Рассмотрим тела качения. Имеем основные технические характеристики закрытых подшипников типоразмера 608: количество тел качения – 7 шт.; диаметр тела качения – 3,969 мм; материал – сталь 52100, плотность стали 7,85 кг/дм3.
Шарик (тело качения) должен соответствовать стандарту ГОСТ 3722-81 степени точности 5. Согласно стандарту отклонение среднего диаметра составляет ±0,025 мм.
Были проведены замеры диаметров 100 тел качения, в результате получен наименьший диаметр – 3,946 и наибольший диаметр – 3,994. Полученные данные запишем в интервальный статистический ряд: (3,946; 3,954], (3,954; 3,962], (3,962; 3,97], (3,97; 3,978], (3,978; 3,986], (3,986; 3,994].
Из стандарта имеем среднюю ожидаемую величину диаметра – 3,969 мм. В результате проведенных замеров имеем среднюю фактическую величину диаметра – 3,97 мм.
Рассчитаем для каждого среднего интервального значения среднюю ожидаемую абсолютную погрешность и среднюю фактическую абсолютную погрешность. Средняя ожидаемая абсолютная погрешность вычисляется по формуле:
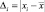
где xi – произведенные замеры; 
– величина диаметра по стандарту. Средняя фактическая абсолютная погрешность вычисляется по формуле:
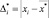
где xi – произведенные замеры;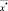 
– средняя фактическая величина диаметра. Получаем:
|
Интервалы |
Среднее интервальное значение |
Ожидаемая абсолютная погрешность |
Фактическая абсолютная погрешность |
|
(3,946; 3,954] |
3,95 |
0,019 |
0,02 |
|
(3,954; 3,962] |
3,958 |
0,011 |
0,012 |
|
(3,962; 3,97] |
3,966 |
0,003 |
0,004 |
|
(3,97; 3,978] |
3,974 |
0,005 |
0,004 |
|
(3,978; 3,986] |
3,982 |
0,013 |
0,012 |
|
(3,986; 3,994] |
3,99 |
0,021 |
0,02 |
Тогда средняя ожидаемая абсолютная погрешность равна: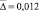 
и средняя фактическая абсолютная погрешность равна: 
.
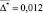Вычислим:
– ожидаемую относительную погрешность:
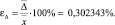
– фактическую относительную погрешность:
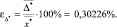
Таким образом, имеем оценку адекватности проведенного исследования:
