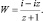Понятие конформного отображения
Теория и практика конформных отображений имеет широкое применение в различных областях: в теории потенциала, в задачах гидродинамики и электростатики, теории упругости.
Во многих случаях возникает проблема сведения задачи, решаемой в некоторой заданной области, к решению ее в другой области. Это – проблема нахождения отображения областей.
Для плоских областей такое отображение
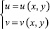
может отображаться в виде w = f(z), u = Ref(z), v = Imf(z), то есть сводится к нахождению соответствующей аналитической функции.
Покажем на примере: найдем дробно-линейную функцию, отображающую круг единичного радиуса с центром в начале координат на верхнюю полуплоскость. То есть требуется найти отображение области D:│z│ < 1 на область G:Im z > 0. Границей области D является окрестность │z│ = 1. Ее образ – прямая. Из теории: окружности и прямые, проходящей через особую точку z = –d/c дробно-линейной функции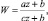 
отображаются в прямые. Поэтому искомая функция должна иметь особую точку одну из точек окружности │z│ = 1.
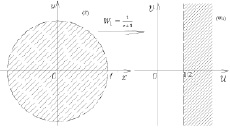
На первом этапе «распрямили» окружность, то есть подберем функцию, переводящую одну из точек окружности в бесконечно удаленную точку.
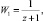
где W1(–1) = ∞. Найдем уравнение прямой, в которую переходит │z│ = 1 при отображении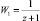 
.
Тогда
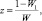
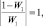
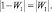
Последнее уравнение задает прямую, перпендикулярную отрезку, соединяющему точки W1 = 1 и W1 = 0, через его середину, то есть ReW1 = 1/2.
Образом области D будет G: ReW1 > 1/2.
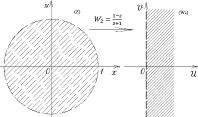
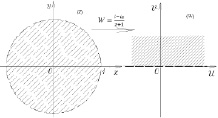
Вторым этапом является смещение (сдвиг) влево на 1/2, то есть линейное отображение W2 = W1 = 1/2. Образом ReW1 = 1/2 будет ReW2 = 0.
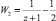или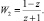 
.
При отображении W2 образом области D является правая полуплоскость ReW2 > 0.
На третьем этапе осуществляется поворот в плоскости W2 на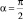 
против часовой стрелки, то есть
, 
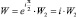