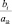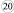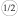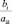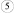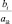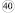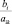Метод искусственного базиса применяется к решению задач линейного программирования в общем случае, когда система ограничений не имеет предпочитаемого вида. Рассмотрим следующий пример.
Задача о диете. Симпатичная девушка узнала из дамского журнала, что для того чтобы волосы стали более шелковистыми, организм должен получать ежедневно не менее 40 г питательного вещества А, не менее 4 г питательного вещества Б и не менее 30 г питательного вещества В. Девушка знает, что в 1 кг яблок содержится 10 г вещества Б и 50 г вещества В, а в 100 г огурцов содержится 40 г вещества А и по 20 г веществ Б и В. Цена яблок – 60 руб. за 1 кг, цена огурцов – 50 руб. за 1 кг. Требуется помочь девушке составить рацион, помогающий увеличить шелковистость волос и при этом имеющий наименьшую стоимость.
Решение. Обозначим x1 и x2 массу приобретаемых девушкой яблок и огурцов, тогда общее количество получаемого в рационе питательного вещества А будет равно 40x2 (г), количество вещества Б в рационе составит 10x1 + 20x2 (г), а количество вещества В составит 50x1 + 20x2 (г). При этом общая стоимость приобретаемых продуктов составит 60x1 + 50x2 руб. Таким образом, получаем следующую задачу линейного программирования:
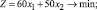
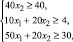
x1 ≥ 0, x2 ≥ 0.
Для превращения системы ограничений в систему уравнений необходимо ввести балансовые неизвестные x3, x4 и x5:
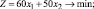
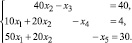
xj ≥ 0, j = 1, 2, 3, 4, 5.
Вновь введённые переменные x3, x4 и x5 нельзя считать базисными, поскольку они соответствуют базисному решению с отрицательными компонентами.
Поэтому введём искусственные базисные неизвестные t1, t2, t3 (M >> 1) и рассмотрим задачу:
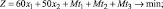
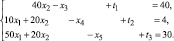
xj ≥ 0, j = 1, 2, 3, 4, 5, t1 ≥ 0, t2 ≥ 0, t3 ≥ 0.
Далее процесс решения проведём в симплексной таблице.
|
cj ci |
БП |
60 |
50 |
0 |
0 |
0 |
М |
М |
М |
Z |
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
t1 |
t2 |
t3 |
b |
|||
|
М |
t1 |
0 |
40 |
–1 |
0 |
0 |
1 |
0 |
0 |
40 |
1 |
|
М |
t2 |
10 |
|
0 |
–1 |
0 |
0 |
1 |
0 |
4 |
0,2 |
|
М |
t3 |
50 |
20 |
0 |
0 |
–1 |
0 |
0 |
1 |
30 |
1,5 |
|
Δj ≤ 0 |
60М–60 |
80М–50 |
–М |
–М |
–М |
0 |
0 |
0 |
74М |
Критерий на минимум не выполнен |
|
|
М |
t1 |
–20 |
0 |
–1 |
2 |
0 |
1 |
0 |
32 |
––– |
|
|
50 |
x2 |
|
1 |
0 |
–1/20 |
0 |
0 |
0 |
1/5 |
2/5 |
|
|
М |
t2 |
40 |
0 |
0 |
1 |
–1 |
0 |
1 |
26 |
13/20 |
|
|
Δj ≤ 0 |
20М–35 |
0 |
–М |
3М–2,5 |
–М |
0 |
0 |
58М + 10 |
Критерий на минимум не выполнен |
||
|
cj ci |
БП |
60 |
50 |
0 |
0 |
0 |
М |
М |
М |
Z |
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
t1 |
t2 |
t3 |
b |
|||
|
М |
t1 |
0 |
40 |
–1 |
0 |
0 |
1 |
0 |
40 |
––– |
|
|
60 |
x1 |
1 |
2 |
0 |
–1/10 |
0 |
0 |
0 |
2/5 |
––– |
|
|
М |
t2 |
0 |
–80 |
0 |
|
–1 |
0 |
1 |
10 |
2 |
|
|
Δj ≤ 0 |
0 |
70–40М |
–М |
5М–6 |
–М |
0 |
0 |
50М + 24 |
Критерий на минимум не выполнен |
||
|
cj ci |
БП |
60 |
50 |
0 |
0 |
0 |
М |
М |
М |
Z |
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
t1 |
t2 |
t3 |
b |
|||
|
М |
t1 |
0 |
|
–1 |
0 |
0 |
1 |
40 |
1 |
||
|
60 |
x1 |
1 |
2/5 |
0 |
0 |
–1/50 |
0 |
3/5 |
3/2 |
||
|
0 |
x4 |
0 |
–16 |
0 |
1 |
–1/5 |
0 |
2 |
––– |
||
|
Δj ≤ 0 |
0 |
40М–26 |
–М |
0 |
-6/5 |
0 |
40М + 36 |
Критерий на минимум не выполнен |
|||
|
cj ci |
БП |
60 |
50 |
0 |
0 |
0 |
М |
М |
М |
Z |
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
t1 |
t2 |
t3 |
b |
|||
|
50 |
x2 |
0 |
1 |
–1/40 |
0 |
0 |
1 |
||||
|
60 |
x1 |
1 |
0 |
1/100 |
0 |
–1/50 |
1/5 |
||||
|
0 |
x4 |
0 |
0 |
–2/5 |
1 |
–1/5 |
18 |
||||
|
Δj ≤ 0 |
0 |
0 |
–13/20 |
0 |
–6/5 |
62 |
Критерий на минимум выполнен |
||||
В пятой симплексной таблице среди Δj нет ни одного положительного числа. Поэтому базисное решение x1 = 1/5 = 0,2, x2 = 1, x3 = 0, x4 = 18, x5 = 0, t1 = 0, t2 = 0, t3 = 0 является оптимальным. Таким образом, оптимальный рацион состоит из 200 г яблок и 1 кг огурцов.