На сегодняшний день, существенно изменился спектр приложений математики, в связи с переходом к рыночным отношениям. Новый период требует качественного повышения экономической грамотности населения, поэтому актуальным в наши дни является вопрос о применении математических формул и задач экономической деятельности.
Основа основ любой экономики – это производство, т. к. оно позволяет людям удовлетворять свои многочисленные потребности. Экономистам все время приходится решать одну глобальную задачу – как можно больше произвести, и при этом, как можно меньше затратить ограниченных ресурсов.
История развития дифференциального исчисления относит нас на несколько веков назад. Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:
1) о разыскании касательной к произвольной линии;
2) о разыскании скорости при произвольном законе движения.
Еще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500–1557 гг.) – здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.
Первый в мире печатный курс дифференциального исчисления опубликовал в 1696 г. Лопиталь. Этот курс состоит из предисловия и 10 глав, в которых излагаются определения постоянных и переменных величин и дифференциала, объясняются употребляющиеся обозначения и др.
В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Жиля Роберваля, английского ученого Джеймса Грегори. Большой вклад в изучение дифференциального исчисления внесли Бернулли, Лагранж, Эйлер, Гаусс.
Дифференциальное исчисление получило широкое применение как математический аппарат для экономического анализа и его развития в экономике.
Базовой задачей экономического анализа является изучение связей экономических величин, записанных в виде функций. В каком направлении изменится доход государства при увеличении налогов или при введении импортных пошлин? Увеличится или уменьшится выручка фирмы при повышении цены на ее продукцию? Для решения подобных задач должны быть построены функции связи входящих в них переменных, которые затем изучаются с помощью методов дифференциального исчисления.
В экономике часто требуется найти наилучшее или оптимальное значение показателей: наивысшую производительность труда, максимальную прибыль, минимальные издержки и т.д. Каждый показатель представляет собой функцию от одного или нескольких аргументов. Таким образом, нахождение оптимального значения показателя сводится к нахождению экстремума функции.
Рассмотрим однофакторную, или одноресурсную, производственную функцию y = f(x), которая дает нам объем производимой продукции за единицу времени в зависимости от объема x затраченного ресурса. Этот ресурс характеризует количество живого человеческого труда, выраженного в виде человеко-часов или числа работников.
Пусть в нынешнем состоянии число работников фирмы равно a. Обычно производственные функции дифференцируемы, так что f(α + 1) ≈ f(α) + f′(α). Если число работников α велико, то данное приближенное равенство довольно точное, но производимая новым сотрудником предприятия за единицу времени.
Пусть v – цена единицы продукции, p – зарплата работника за единицу времени. Тогда, если v∙f′(α) > p, то надо нанять еще одного сотрудника, так как он приносит фирме больше, чем она ему платит. Это несложное правило имеет универсальный характер и называется золотым правилом экономики. Вообще в рассматриваемой ситуации производную производственной функции в точке α в экономике называют предельной производительностью труда (при размере фирмы α), в отличие от средней, которая равна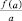 
Рассмотрим некоторые экономические функции и определим экономический смысл их производных.
Функция спроса D = D(p) – зависимость спроса D на некоторый товар от его цены p. Производная D(p) дает приблизительно увеличении цены на одну единицу. Поскольку, как известно, при повышении цены спрос уменьшается, то на самом деле абсолютное значение производной показывает уменьшение спроса со стороны покупателей на товар при повышении его цены на одну единицу.
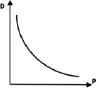
Функция предложения S = S(p) – зависимость предложения некоторого товара от его цены p. Производная дает приблизительно увеличение предложения товара со стороны продавцов (производителей) при увеличении цены на одну единицу.
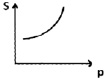
Функция полезности u(x) – субъективная числовая оценка данным индивидом полезности количества x товара для него. Производная u′(x) дает приблизительную оценку дополнительной полезности от приобретения еще одной единицы товара.
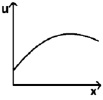
Налоговая ставка – зависимость налога N в процентах от величины годового дохода Q. Пусть P – само значение налога, которое надо платить с годового дохода Q. Тогда производная P и есть налоговая ставка N.
Производная функции y = f(x) дает величину мгновенной скорости изменения пройденного за время x пути y, производная производственной функции дает предельную производительность труда и т.д. Но в экономике чрезвычайно удобно задавать такие вопросы: насколько процентов изменится спрос на товар, если цена на него увеличится на 1 %? На сколько процентов изменится предложение товара, если цена на него увеличится на 1 %? и т.д. Такие вопросы и ответы на них вводят новое понятие эластичность функции по аргументу, или относительная производная.
Рассмотрим функцию y = f(x). Пусть Δx – приращение аргумента, Δf(x) – соответствующее приращение функции. Тогда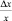 
– относительное изменение аргумента, 
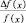– относительное изменение функции. Величина 
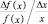– отношение относительного изменения функции к относительному изменению аргумента – называется средней эластичностью функции по аргументу на отрезке [x, x + Δx],а предел этого отношения при Δx → 0x, т.е.
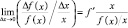
называется эластичностью функции y по аргументу в точке x и обозначается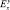 
.
Например. Для функции спроса D = 40 – 2p найти эластичность спроса по цене при p = 4.
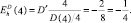
Решение:
Рассмотрим роль производной в экономике на примере. Нам нужно узнать какова максимальная выручка монополиста, если спрос вплоть до пересечения с осями описывается линейной функцией Q = b – ap, где p – цена товара, выпускаемого монополистом; a и b – коэффициенты функции спроса?
Выручка TR = Qp = p(b – ap) достигнет максимума при равенстве нулю производной по цене: TR′ = (p(b – ap))′ = 0.
TR′ = p′∙(b – ap) + (b – ap)′∙p == b – ap – ap = b – 2ap = 0;
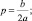
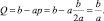
При этом максимум выручки составит
Экономический смысл производной заключается в следующем: производная является важнейшим инструментом экономического анализа, позволяющим углубить геометрический и математический смысл экономических понятий, а также выразить ряд экономических законов с помощью математических формул. С ее помощью решаются важнейшие экономические задачи. На практике производная служит очень хорошим инструментом при решении задач оптимизационного характера: на производительность труда, эластичность спроса и др. Из этого следует вывод, что производная играет важную роль в экономике.