Загрязнение окружающей среды – побочный продукт обычной экономической деятельности.
Побочные продукты (как ценные, так и неценные) непосредственно связанны с системой физических взаимодействий, определяющих повседневное функционирование экономической системы. Техническую взаимозависимость между уровнями выпуска желательных и нежелательных продуктов, можно описать в терминах коэффициентов, которые используются для выявления взаимозависимости между всеми обычными отраслями производства и потребления. Поэтому побочные продукты производственной деятельности и потребления следует рассматривать как часть экономической системы. Модель, учитывающая экологический фактор известна как модель Леонтьева-Форда [1]:
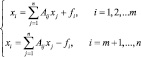
Рассмотрим модель межотраслевого баланса, в которой учтены требования экологии
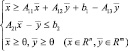(1)
представляющей из себя систему линейных неравенств.
Рассмотрим случай, когда A13(y) ≠ θ. В этом случае модель Леонтьева – Форда имеет вид:
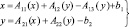(2)
и предусматривает утилизацию вредных отходов. Решение этой системы обозначим через 
, 
(если это решение существует).
Для нахождения решения данной системы используется теорема:
Теорема 1. Пусть (x2, y2) – решение системы (2) – с утилизацией вредных отходов, (x1, y1) – решение системы
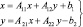(3)
без утилизации вредных отходов. Тогда справедливо неравенство
(x2, y2) ≤ (x1, y1).
Приближенное решение модели Л-Ф
Рассмотрим алгоритм приближенного решения уравнений вида
x = A1x + A2x + f, (4)
где A1 – монотонно возрастающий оператор; A2 – монотонно убывающий оператор, ибо модель (2) является моделью именно такого вида, т.е. A1↑, A2↓. Можно доказать утверждение:
Теорема 2. Пусть A1, A2 – монотонные относительно конуса K операторы, причем A1↑, A2↓ и существуют такие два элемента u0, v0 (u0 < v0), для которых выполняется условие
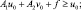(5)
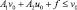(6)
относительно конуса. Тогда для un, vn, определенных формулами
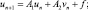(7)
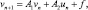(8)
где (n = 0, 1, ...), справедливы неравенства
un ≤ un+1; vn ≤ vn+1.(9).
Тогда вектор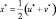 
является решением уравнения (4).
Границы u1, v1 решения x* можно заметно сблизить, если воспользоваться следующим результатом Стеценко В.Я., приведенного в [4].
Теорема 3. Пусть в условиях теоремы 2 число m ≥ 0 таково, что u1 – u0 ≥ m(v1 – v0); v0 – v1 ≥ m(u1 – u0).
Тогда для решения x*справедливо неравенство
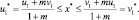(10)
При этом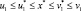 
.
Формулу (10) можно рассматривать как рекуррентный процесс построения последовательностей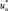 
, 
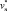. Последовательности 
, 
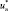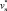монотонно по недостатку и по избытку (соответственно) сходятся к x*, и, как правило, существенно быстрее, чем un, vn.
Приведем еще пример построения монотонных приближений к решению на этот раз для случая задачи Коши для обыкновенного дифференциального уравнения.
Рассмотрим задачу Коши: найти решение дифференциального уравнения
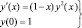(11)
Перейдем от этой задачи Коши к следующему эквивалентному интегральному уравнению
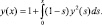(12)
Эквивалентность понимается здесь в том смысле, что каждое непрерывное решение уравнения (12) является решением задачи (11). Заметим, что в промежутке (0; 1) подынтегральная функция в правой части (12) положительная, а на (1; +∞) – отрицательная. Поэтому оператор
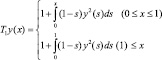(13)
возрастающий, а оператор
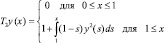(14)
убывающий. При этом задача (11) принимает вид
y = Ty(x), (15)
где T = T1 + T2, причем T1↑, а T2↓. Для приближенного решения уравнения (11) можно воспользоваться методом
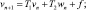
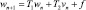(n = 0, 1, ...)
где v0 и w0 таковы, что
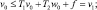
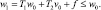
Обозначим через m ≥ 0 такую постоянную, для которой
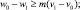
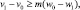(16)
и положим
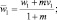
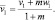(17)
Тогда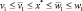 
.
Т.е. 
и 
располагаются к решению x* уравнения x = Tx + f, вообще говоря, намного ближе, чем v1 и w1. Переход от v1, w1 к 
, 
согласно формулам (16), (17) представляет способ ускорения сходимости приближений к решению x*.