Одними из перспективных материалов для тонких поглощающих солнечную энергию слоёв в фотовольтаических структурах являются кестериты Cu2ZnSn(S,Se)4. Эти четверные соединения являются прямозонными полупроводниками с шириной запрещённой зоны 1-1,5 эВ и большим коэффициентом поглощения (~ 104 см-1) [1, 2]. Несомненным преимуществом этих материалов является низкая цена и отсутствие токсичности. Возможно, со временем эти материалы составят конкуренцию дорогим высокопоглощающим слоям CuIn1−xGaxSe2 используемым в солнечных элементах и демонстрирующим эффективность ~ 20 % [3]. Cu2ZnSnS4 так же привлекает интерес исследователей как термоэлектрический материал и материал фотокатода для извлечения водорода из воды [4, 5].
Основными для Cu2ZnSnS4 являются структуры кестерита с пространственной группой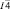 
и станнита c пространственной группой 
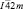. В этих структурах подрешетки, занятые атомами S одинаковы, а атомы металлов размешаются по разному. В структуре кестерита чередуются слои Сu–Sn и Cu-Zn, а в структуре станнита слои Zn–Cu и Cu–Cu [6].Было установлено, что наиболее стабильной структурой для Cu2ZnSnS4 является структура кестерита, но разница в полной энергии со структурой станнита невелика [6].
В настоящей работе описана технология получения и приведены результаты исследования температурных зависимостей электропроводности поликристаллических образцов Cu2ZnSnS4.
Эксперимент
Синтез кестерита Cu2ZnSnS4 был осуществлён методом пиролитического разложения стехиометрической смеси солей CuCl2·2H2O (0,01 M), ZnCl2 (0,005 M), SnCl2·2H2O (0,005 M) и тиомочевины SC(NH2)2 предварительно растворенных в 50 %-м спиртовом растворе. Полученный раствор был подвергнут сушке при температуре 70-80 °С в течении 30 часов. Затем материал был измельчён. Полученный порошок подвергался отжигам в печи при температуре 400-450 °С в течении часа в слабом вакууме для полного удалении Cl2.
Cu2ZnSnS4 был получен по следующей реакции:
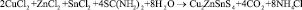
Был проведен рентгенофазовый анализ образца на диффрактометре Rigaku IV на порошке, съёмка θ –2θ, в диапазоне углов 10-100 град., шаг 0,04 град., скорость 2 град./мин, фильтр Ni (Kβ), Cu Kα λ = 1,54056 Å, без монохроматора, в геометрии Брен-Брентано. Полученная порошковая диффрактограмма приведена на рис. 1.
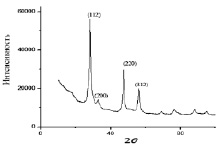
Рис. 1. Спектр порошковой дифракции образца Cu2ZnSnS4
Основные пики на рис. 1 совпадают по положению и относительной интенсивности с полученными в работах [7, 8]. Что подтверждает факт синтеза кестерита Cu2ZnSnS4.
Электропроводность была исследована на прессованных поликристаллических образцах в форме параллелепипеда 2,6×7,8×1,4 мм3. Измерения были проведены стандартным четырёхзондовым методом в диапазоне температур от 10 до 320 К.
Результаты и обсуждение
На рис. 2 представлены результаты исследования четырёхзондовым методом температурной зависимости удельного сопротивления в диапазоне температур от 10 до 300 К. Как видно из рис. 2, с понижением температуры удельное сопротивление возрастает. Для описания электропроводности в сильно легированных, неупорядоченных и аморфных полупроводниках часто привлекают различные механизмы прыжковой проводимости.
Согласно существующим теоретическим представлениям, температурная зависимость удельного сопротивления ρ(T) в режиме прыжковой проводимости описывается универсальным законом [9, 10]:
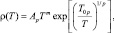(1)
где Ap постоянный предэкспоненциальный множитель, T0p является характерной прыжковой температурой, р = 1 соответствует механизму проводимости по ближайшим соседям; в режиме прыжковой проводимости с переменной длиной прыжка (ПППДП) р = 4 при механизме Мотта, а р = 2 соответствует проводимости типа Шкловского – Эфроса (ШЭ) [10].
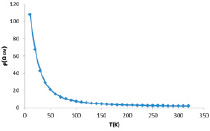
Рис. 2. Температурная зависимость удельного сопротивления Cu2ZnSnS4
Температурная зависимость удельного сопротивления Cu2ZnSnS4 в координатах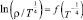 
при понижении температуры в диапазоне от Tm ≈ 60 K до Tv ≈ 180 K зависимость становится линейной, что прекрасно согласуется с законом Мотта. Вычисленная из наклона этой зависимости величина T04 составила 2,5∙104.
Важный параметр, определяющий проводимость:
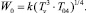(2)
Из формулы (2) получаем W0 = 50,1 мэВ. Этот параметр связан с шириной примесной зоны, W ≈ W0/2. Полученное значение W0 сопоставимо с полученным на образцах Cu2ZnSnS4 в [11], где для некоторых образцов Cu2ZnSnS4 достигало W0 = 45,1 мэВ.
Заключение
Таким образом, нам удалось синтезировать кестерит Cu2ZnSnS4 и провести рентгенофазовый анализ, подтверждающий результаты синтеза. В настоящей работе были исследованы температурные зависимости электропроводности поликристаллических образцов Cu2ZnSnS4. Анализ этих зависимостей показывает, что поведение сопротивления образца Cu2ZnSnS4 в температурном интервале 60-180 K подчиняется механизму прыжковой проводимости Мотта с переменной длиной прыжка.
Часть результатов приведенных в настоящей работе была получена в рамках выполнения Государственного задания 2.3309.2011.