Научно-техническое решение относится к дендрометрии при изучении относительного сбега комля в ходе роста и развития деревьев, преимущественно берез, и может быть использовано при фитоиндикации качества территорий и разработке мероприятий по защите земельных участков от эрозии, а также в дендроэкологическом мониторинге за развитием овражной сети с учетом изменений относительной формы комля растущих деревьев.
Известен способ анализа комля древесного ствола по патенту № 2254707 [4], включающий разметку ствола на секции кратной или некратной длины в зависимости от расположения неровностей ствола с измерением расстояний от корневой шейки, секции некратной длины размечают на неровностях комлевой части, по крайней мере, дважды в трех точках неровности, а измерения вдоль и поперек ствола по секциям выполняют гибкой мерной лентой, причем поперек ствола измеряют гибкой мерной лентой периметр сечения ствола.
Недостатком является то, что измерения выполняют у деревьев, растущих на ровной местности. При этом известный способ не позволяет учитывать влияние периметров комля ниже корневой шейки деревьев. Причем березы могут произрастать на склоне оврага, сильно изменяя высоту корневой шейки от точки склона по середине ствола.
Известен также способ анализа комля растущего дерева для определения поперечного профиля оврага по патенту № 2416193 РФ [5], характеризующийся тем, что поперек оврага выбирают пробную полосу леса с расположенными вдоль нее деревьями, измеряют расстояния и общий угол склона в поперечном сечении оврага между серединами диаметров корневой шейки смежных вдоль пробной полосы деревьев.
Недостатком также является отсутствие измерений периметра комлевой части дерева ниже корневой шейки, что не позволяет изучать влияние склона оврага или холма на комлевую часть, начиная на стволе от высоты 1,3 м над корневой шейкой до поверхности почвы на склоне оврага или холма.
Кроме того, в дендрометрии до сих пор не выделены те лимитирующие факторы комля, которые влияют на параметры места произрастания дерева.
Технический результат – расширение функциональных возможностей анализа по относительному сбегу комлевой части деревьев, произрастающих на склоне оврага или холма, а также повышение точности измерений березы ниже корневой шейки, начиная от стандартной высоты ствола в 1,3 м над корневой шейкой дерева до поверхности склона оврага.
Сущность технического решения заключается в том, что наиболее часто на склонах оврагов в лесостепной зоне России произрастают березы естественного происхождения. Они закрепляют овраги от водной эрозии, и происходит симбиоз между березняком и почвой на склоне оврага: березы своими корнями защищают почву от смыва, а почва наращивает свою плодородие, позволяя расти березам продуктивно без потери питательных веществ. Такой симбиоз приводит к относительному изменению поперечных сечений комля деревьев.
Сущность технического решения заключается также в том, что береза обладает замечательным свойством стать древесным растением для дендроэкологического мониторинга [1-3] из-за повсеместного произрастания на нарушенных человеком земельных участках, подверженных ветровой и водной эрозии, и предотвращает развитие овражной сети.
Сущность технического решения заключается также и в том, что в некоторых природно-антропогенных условиях частично восстанавливается и полноводность и регулярность водотока в течение года на дне оврага.
Сущность технического решения заключается также и в том, что отношения между периметрами сечений на разных уровнях по высоте комля показали наибольшую тесноту факторной связи между собой и от стандартного диаметра на высоте 1,3 м.
Положительный эффект достигается выявлением закономерностей по трем относительным показателям: P1.3 /D1.3 – коэффициент формы поперечного сечения ствола дерева на стандартной высоте 1,3 м; Pкш / P1.3 – относительный сбег поперечного сечения ствола дерева от корневой шейки до стандартной высоты 1,3 м, то есть коэффициент закомелистости ствола дерева; Ph / P1.3 – относительный сбег комля дерева от сечения на высоте комля до стандартной высоты над корневой шейкой дерева.
Эти показатели позволяют проводить экологический мониторинг за состоянием и развитием изучаемого березняка, что показано на фигурах 1-7.
На рис. 1 приняты следующие условные обозначения: j – угол местного склона в месте произрастания дерева березы, град; D1.3 , P1.3 – диаметр и периметр ствола на высоте 1,3 м от корневой шейки; Pкш – периметр сечения ствола на корневой шейке, см; 0,5 P3 – половина периметра комля над точкой пересечения поверхности почвы с вертикальной осевой линией комля, см; h – высота комля от корневой шейки до точки пересечения поверхности почвы с вертикальной осевой линией комля, см; hmax – максимальная высота комля от корневой шейки до нижней точки пересечения поверхности почвы с боковой линией комля, см.
Способ анализа относительного сбега комля выполняется следующими действиями.
Вначале выбирают пробную площадь и на ней не менее 30 учетных деревьев одной породы, например, березы.
При этом пробная площадь может быть заложена на любой неровной и холмистой местности, а также на склонах оврагов, террас или берегов.
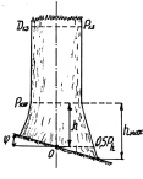
Рис. 1. Схема измерения параметров комля
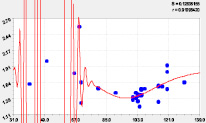
Рис. 2. График влияния максимальной высоты комля 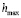 на относительный сбег комля
на относительный сбег комля 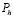 /
/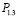
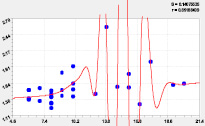
Рис. 3. Влияние высоты кроны Hкр на относительный сбег Ph /P1.3
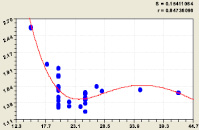
Рис. 4. Влияние диаметра ствола D1.3 на показатель Ph /P1.3
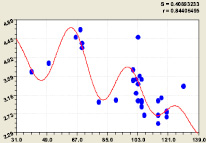
Рис. 5. Влияние максимальной высоты комля hmax на показатель P1.3/ D1.3
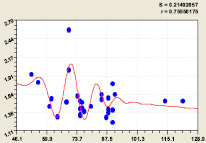
Рис. 6. Влияние периметра ствола P1.3 на показатель Ph / P1.3
У каждого учетного дерева на стандартной высоте 1,3 м измеряют диаметр и одновременно периметр поперечного сечения ствола.
Комель принимают в виде симметричной геометрической фигуры, расположенной вдоль вертикальной оси ствола учетного дерева. Высоту комля у каждого учетного дерева измеряют от поперечного сечения комля на корневой шейке до точки пересечения вертикальной оси с поверхностью почвы.
Затем от этой точки до периферии комля на нижней стороне по склону измеряют полупериметр нижнего поперечного сечения комля, После этого с учетом местного угла склона у каждого учетного дерева дополнительно измеряют максимальную высоту комля от корневой шейки ствола до поверхности почвы на нижней стороне по склону. А по множеству измеренных берез выполняют расчеты относительных показателей и проводят статистическое моделирование идентификацией многочленной однофакторной математической модели.
При необходимости у учетного дерева измеряют также периметр поперечного сечения начала комля на корневой шейке ствола учетного дерева.
От точки пересечения вертикальной оси с поверхностью почвы до периферии комля на нижней стороне по склону полупериметр поперечного сечения комля измеряют гибкой мерной лентой. Причем измерения проводят между двумя точками пересечения линии вдоль склона оврага, проходящей через точку пересечения вертикальной оси ствола учетного дерева с поверхностью почвы.
По множеству измеренных берез выполняют расчеты следующих относительных показателей по формулам:
P1.3/ D1.3 – коэффициент формы поперечного сечения ствола дерева на стандартной высоте 1,3 м;
Pкш / P1.3 – относительный сбег ствола дерева от корневой шейки до стандартной высоты 1,3 м, то есть коэффициент закомелистости ствола дерева;
Ph / P1.3 – относительный сбег комля дерева от сечения на высоте комля до стандартной высоты над корневой шейкой дерева.
По измеренным данным выполняют частный факторный анализ влияния измеренных параметров учетных деревьев на отношения меду периметрами поперечных сечений комля.
Пример. Для снижения линейной эрозии почвы оврагами применяют растения. Цель исследования – изучение формы комля деревьев, растущих в овраге, для выявления закономерностей взаимодействия между древесными растениями и склоном.
Объектами исследования были выбраны березы на склоне лесного оврага около деревни Ямолино Горномарийского района Республики Марий Эл. Эксперименты были проведены летом 2011 года (табл. 1) на 30 березах.
Измерения комля дерева выполняется следующим образом (рис. 1).
Сначала определили участок оврага по методике, изложенной в патенте № 2416193 РФ по прототипу, на склоне которого растут деревья. Выбрали учетные деревья для измерений в количестве 30 штук. Для измерений применяли гибкую мерную ленту и транспортир с отвесом. В ходе моделирования идентификацией устойчивых законов было выявлено, что дерево № 6 имеет резко выделяющееся значение угла местного склона. В дальнейшем это наблюдение исключили из статистической выборки.
Таблица 1
Параметры деревьев и периметры сечения комля с их отношениями
|
№ п/п |
D1.3, см |
h, см |
hmax, см |
Hкр, м |
H, м |
Периметр сечения, см |
P1.3/ D1.3 |
Pкш / P1.3 |
Ph / P1.3 |
||
|
P1.3 |
Pкш |
0,5 Ph |
|||||||||
|
1 |
20 |
81 |
70 |
20 |
25 |
85 |
87 |
70 |
4.25 |
1.024 |
1.647 |
|
2 |
20 |
64 |
66 |
15 |
24 |
90 |
95 |
81 |
4.50 |
1.056 |
1.800 |
|
3 |
15 |
60 |
69 |
13 |
19 |
70 |
75 |
90 |
4.67 |
1.071 |
2.571 |
|
4 |
18 |
35 |
50 |
17 |
24 |
70 |
80 |
70 |
3.89 |
1.143 |
2.000 |
|
5 |
20 |
36 |
40 |
19 |
25 |
74 |
79 |
60 |
3.70 |
1.068 |
1.622 |
|
7 |
20 |
40 |
70 |
16 |
20 |
87 |
90 |
57 |
4.35 |
1.034 |
1.310 |
|
8 |
25 |
48 |
80 |
10 |
16 |
75 |
85 |
58 |
3.00 |
1.133 |
1.547 |
|
9 |
20 |
36 |
90 |
12 |
20 |
61 |
71 |
45 |
3.05 |
1.164 |
1.475 |
|
10 |
35 |
40 |
115 |
14 |
25 |
88 |
110 |
70 |
2.51 |
1.250 |
1.591 |
|
11 |
20 |
40 |
120 |
9 |
18 |
56 |
72 |
51 |
2.80 |
1.286 |
1.821 |
|
12 |
24 |
41 |
115 |
8 |
15 |
65 |
67 |
43 |
2.71 |
1.031 |
1.323 |
|
13 |
20 |
35 |
120 |
10 |
20 |
53 |
81 |
51 |
2.65 |
1.528 |
1.925 |
|
14 |
20 |
45 |
117 |
15 |
19 |
62 |
75 |
49 |
3.10 |
1.210 |
1.581 |
|
15 |
27 |
38 |
130 |
10 |
18 |
91 |
110 |
75 |
3.37 |
1.209 |
1.648 |
|
16 |
28 |
45 |
115 |
7 |
15 |
85 |
101 |
67 |
3.04 |
1.188 |
1.576 |
|
17 |
25 |
40 |
120 |
9 |
15 |
69 |
83 |
53 |
2.76 |
1.203 |
1.536 |
|
18 |
25 |
45 |
105 |
8 |
14 |
76 |
98 |
58 |
3.04 |
1.289 |
1.526 |
|
19 |
42 |
40 |
105 |
6 |
16 |
122 |
140 |
94 |
2.90 |
1.148 |
1.541 |
|
20 |
42 |
43 |
107 |
6 |
15 |
114 |
135 |
88 |
2.71 |
1.184 |
1.544 |
|
21 |
25 |
50 |
105 |
8 |
15 |
88 |
100 |
63 |
3.52 |
1.136 |
1.432 |
|
22 |
25 |
51 |
104 |
8 |
16 |
90 |
96 |
56 |
3.60 |
1.067 |
1.244 |
|
23 |
22 |
60 |
100 |
6 |
16 |
77 |
85 |
54 |
3.50 |
1.104 |
1.403 |
|
24 |
20 |
65 |
100 |
7 |
15 |
75 |
76 |
51 |
3.75 |
1.013 |
1.360 |
|
25 |
25 |
71 |
102 |
6 |
16 |
88 |
91 |
61 |
3.52 |
1.034 |
1.386 |
|
26 |
22 |
65 |
103 |
8 |
17 |
75 |
80 |
50 |
3.41 |
1.067 |
1.333 |
|
27 |
25 |
55 |
102 |
8 |
20 |
80 |
90 |
59 |
3.20 |
1.125 |
1.475 |
|
28 |
20 |
70 |
103 |
8 |
20 |
90 |
108 |
64 |
4.50 |
1.200 |
1.422 |
|
29 |
25 |
62 |
105 |
10 |
20 |
75 |
84 |
54 |
3.00 |
1.120 |
1.440 |
|
30 |
25 |
63 |
103 |
9 |
20 |
76 |
81 |
55 |
3.04 |
1.066 |
1.447 |
Примечание. Дерево № 6 исключено из-за резкого отклонения угла местного склона.
Полученные данные из табл. 1 обрабатывали в программной среде CurveExpert-1.3 по общей детерминированной модели
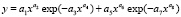 , (1)
, (1)
где y – показатель или зависимый фактор, в нашем примере параметры по табл. 1; x – объясняющая переменная или влияющий фактор, приведены также в табл. 1; a1… a8 – параметры модели (1), получаемые идентификацией в программной среде CurveExpert1.38 или 1.40.
Эта двухчленная формула в каждом случае выявления закономерности была получена идентификацией устойчивых законов по табл. 2. При этом первая составляющая, как правило, показывает естественный процесс или явление, а вторая и последующие члены формулы (1) характеризуют, как правило, антропогенное влияние. Во многих случаев антропогенное влияние имеет характер колебательного возмущения.
По принципу «от простого к сложному» можно предложить (табл. 2) «кирпичики» для построения, по ходу структурно-параметрической идентификации биотехнического закона, любой статистической модели.
Таблица 2
Математические конструкты для построения статистической модели
|
Фрагменты без предыстории изучаемого явления или процесса |
Фрагменты с предысторией изучаемого явления или процесса |
|
|
|
|
|
|
|
|
|
|
|
|
В табл. 2 показаны все «нормальные» фрагменты, у которых впереди могут быть расположены оперативные константы, в виде знаков «+» или «–». Все шесть устойчивых законов распределения являются частными случаями биотехнического закона, показанного внизу табл. 2.
Далее примем правила отбора тех или иных бинарных факторных связей типа (1) для последующего математического и графического анализа.
В табл. 3 приведены интервалы изменения коэффициента корреляции при различных характеристиках связи между учтенными факторами.
Таблица 3
Уровни факторных связей по коэффициенту корреляции
|
Интервал коэффициента корреляции |
Характер тесноты связи между переменными факторами |
||
|
Существующая классификация |
Для технических экспериментов |
Уточненная шкала для комля дерева |
|
|
1 |
сильная связь |
однозначная |
однозначная |
|
0,99…1,00 |
сильнейшая |
почти однозначная |
|
|
0,95…0,99 |
сверхсильная |
||
|
0,90…0,95 |
сильнейшая |
||
|
0,7…0,9 |
сильная |
сильная |
|
|
0,5…0,7 |
слабая связь |
средняя |
средняя |
|
0,3...0,5 |
слабоватая |
слабоватая |
|
|
0,1…0,3 |
нет связи |
слабая |
слабая |
|
0,0…0,1 |
слабейшая |
слабейшая |
|
|
0 |
нет связи |
нет связи |
|
Как известно из классической математической статистики, грубая классификация уровней коэффициента корреляции следующая:
а) до 0,3 – нет связи между факторами (то есть можно не учитывать эти связи, хотя они в других условиях проявления могут оказаться даже сильными по факторной связи);
б) от 0,3 до 0,7 – есть связь между двумя факторами, но она считается достаточно слабой, чтобы её учитывать в практических рекомендациях;
в) выше 0,7 – имеется сильная связь между переменными факторами даже при не волновых биотехнических закономерностях.
Однако существующая шкала квантификации тесноты связи является очень грубой. Поэтому нами была предложена для технических экспериментов, в которых погрешность измерений не превышает 5 %, другая шкала (третий столбец табл. 3). Но для комля деревьев пришлось ввести еще два интервала, что нами было выполнено только при моделировании распределений рядов простых чисел. Это указывает на высокий уровень проявления закономерности (1) на параметрах комля березовых деревьев.
В табл. 4 приведены результаты факторного влияния (по исходным данным из таблицы 1) на значения относительных параметров комля.
На первом месте как влияющая переменная оказалась максимальная высота комля, что указывает на высокую значимость комлевой части для жизнедеятельности всего дерева. Только на втором месте оказался стандартный диаметр на высоте 1,3 м. Как зависимый показатель на первом месте находится коэффициент формы поперечного сечения ствола дерева на стандартной высоте 1,3 м.
Коэффициент коррелятивной вариации для всего множества влияния 7 влияющих переменных на три показателя равен 9,4074 / 21 = 0,4480.
Таблица 4
Факторный анализ влияния параметров берез на относительные показатели по детерминированным биотехническим закономерностям
|
Параметра дерева (влияющий фактор x) |
Относительные параметры комля |
Сумма коэфф. корр. |
Место Ix |
||
|
P1.3/ D1.3 |
Pкш / P1.3 |
Ph / P1.3 |
|||
|
Угол местного склона j, град |
0,092 |
0,200 |
0,288 |
0,5800 |
7 |
|
Диаметр ствола D1.3, см |
0,661 |
0,134 |
0,8474 |
1,6424 |
2 |
|
Периметр ствола P1.3, см |
0,479 |
0,7380 |
0,288 |
1,5050 |
3 |
|
Высота комля h, м |
0,576 |
0,517 |
0,335 |
1,4280 |
5 |
|
Максимальная высота комля hmax, м |
0,673 |
0,597 |
0,617 |
1,8870 |
1 |
|
Высота дерева березы H, м |
0,360 |
0,131 |
0,371 |
0,8620 |
6 |
|
Высота кроны березы Hкр, м |
0,486 |
0,461 |
0,556 |
1,5030 |
4 |
|
Сумма коэффициента корреляции |
3,3270 |
2,7780 |
3,3024 |
9,4074 |
– |
|
Место Iy параметров модели |
1 |
3 |
2 |
– |
0,4480 |
Этот критерий (термин «коррелятивная вариация» по Ч. Дарвину) применяется при сравнении различных биологических объектов исследования, в данном случае группы из 29 берез, причем так можно сравнивать не только деревья и их группы в разных экологических условиях, но и растительные сообщества, находящие в разных регионах произрастания.
Поэтому факторный анализ, проведенный по показателям одного и того же объекта, имеет многогранное применение. Главное условие для факторного анализа, это добротность и достоверность исходных данных. Тогда можно ожидать хороших результатов по выявлению биотехнических закономерностей между отдельными количественными факторами.
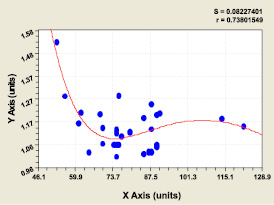
Рис. 7. Влияние периметра ствола P1.3 на показатель Pкш / P1.3
Из данных табл. 4 видно, что наибольшую тесноту связи с коэффициентом корреляции 0,8474 имеет влияние диаметра D1.3 на изменение отношения периметров Ph / P1.3, то есть влияния на относительный сбег комля дерева до высоты 1,3 м над поверхностью почвы.
Таким образом, экологическая таксация деревьев коренным образом отличается от технической таксации стволов на древесину в виде кругляка.
Поэтому предлагаемый способ может быть применен в индикации не только лесных деревьев, но и фитоиндикации неровных мест произрастания древесных растений, в частности, на склонах оврагов, террас и берегов.




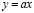 – закон линейного роста или спада (при отрицательном знаке перед правой стороной приведенной формулы)
– закон линейного роста или спада (при отрицательном знаке перед правой стороной приведенной формулы)
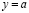 – закон не влияния принятой переменной на показатель, который имеет предысторию значений
– закон не влияния принятой переменной на показатель, который имеет предысторию значений
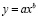 – закон показательного роста (закон показательной гибели
– закон показательного роста (закон показательной гибели 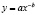 не является устойчивым, из-за бесконечности при нулевом значении объясняющей переменной
не является устойчивым, из-за бесконечности при нулевом значении объясняющей переменной
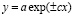 – закон Лапласа (Ципфа в биологии, Парето в экономике, Мандельброта в физике) экспоненциального роста или гибели, относительно которого создан метод операторных исчислений
– закон Лапласа (Ципфа в биологии, Парето в экономике, Мандельброта в физике) экспоненциального роста или гибели, относительно которого создан метод операторных исчислений
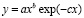 – биотехнический закон в упрощенной форме
– биотехнический закон в упрощенной форме
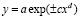 – закон экспоненциального роста или гибели, – по П.М. Мазурикну
– закон экспоненциального роста или гибели, – по П.М. Мазурикну
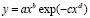 – биотехнический закон, предложенный проф. П.М. Мазуркиным
– биотехнический закон, предложенный проф. П.М. Мазуркиным