Величина зерна – важнейший структурный фактор, определяющий сопротивление металла хрупкому разрушению при понижении температуры. Механизмы разрушения сталей с учетом размера зерна рассмотрены в известных работах Петча, Коттрелла, Стро и др. [1]. В соответствии с дислокационной теорией разрушения увеличение размера зерна обусловливает повышение локальной концентрации напряжений у границ зерна, что должно приводить к понижению напряжения хрупкого разрушения и повышению критической температуры хрупкости. Несмотря на понимание влияния размера зерна на температуру хладноломкости стали, не было перехода от оценки температуры хладноломкости образцов к температуре хладноломкости деталей с концентраторами напряжений. Однако, был разработан подход, позволяющий по результатам испытаний стандартных образцов с помощью метода конечных элементов оценить температуру хладноломкости деталей [2]. В то же время, для проектирования ответственных деталей на стадии проектирования требуется учет структуры стали, в том числе размера зерна. Полагали, что использование критерия критических локальных растягивающих напряжений и критерия хладноломкости [3] позволит выяснить закономерности влияния размера зерна на сопротивление хрупкому разрушению при понижении температуры с позиций структурной механики разрушения и, на этой основе, разработать способ прогнозирования критической температуры хрупкости по известному размеру зерна.
Целью работы являлось количественное моделирование зависимости температуры хладноломкости образцов и деталей с концентраторами напряжений от размера зерен стали на основе применения метода математического моделирования напряженно-деформированного состояния в зоне зарождения трещины.
В качестве материала исследования использовали сталь 10кп. Путем применения различных термообработок были получены различные состояния стали, различающиеся средним размером зерен: 11, 28, 45 и 60 мкм. Использовали цилиндрические образцы без надреза и с надрезами для испытаний на растяжение. Испытания проводили в диапазоне температур 77–293 К. Определение температуры хладноломкости заключалось в установлении температуры, при которой разрушающая нагрузка равна нагрузке общей текучести. Принимая во внимание микрофрактографическую картину распространения трещины сколом, полагали, что процесс разрушения образцов стали 10 кп с различным размером зерна при температурах ниже критических температур хрупкости контролируется критическим максимальным локальным растягивающим напряжением. По результатам испытаний гладких цилиндрических образцов строили зависимости предела текучести стали от температуры испытаний стали для различных размеров зерен. Были получены кривые зависимости предела текучести от температуры испытаний для различных размеров зерна (11, 28, 45 и 60 мкм). Для расчета максимальных локальных растягивающих напряжений использовали метод математического моделирования напряженно-деформированного состояния в зоне зарождения трещины перед концентратором напряжений – метод конечных элементов. С одной стороны этот метод использовали для расчета локальных напряжений в зоне зарождения трещины в экспериментальных образцах, с другой, для расчета локальных напряжений в исследуемой детали с концентраторами напряжений.
Определяли критические максимальные локальные растягивающие напряжения для образцов по ранее изложенной методике [4], заключающейся в установлении температуры совпадения нагрузок разрушающей и общей текучести и, далее, расчете критического максимального локального растягивающего напряжения по формуле:
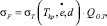(1)
где QО.Т – перенапряжения общей текучести;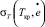 
– предел текучести при критической температуре хрупкости; d – размер зерна. Экспериментальную зависимость критического максимального локального растягивающего напряжения – σF (Н/мм2) от размера зерна – d (мм) стали 10 кп аппроксимировали выражением:
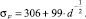(2)
Было установлено, что существует связь температуры хладноломкости с критическим максимальным локальным растягивающим напряжением, пределом текучести и перенапряжением общей текучести, учитывающим скорость нагружения, способ нагружения, геометрию концентратора напряжений и образца:
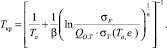(3)
С другой стороны, критическое максимальное локальное растягивающее напряжение σF и предел текучести стали σT зависят от размера зерна. Однако σF не зависит от температуры испытаний, а предел текучести σT зависит. Поэтому представляется возможным связать температуру хладноломкости непосредственно с размером зерна, учитывая геометрию концентратора напряжений, способ и скорость нагружения. Для практических целей прогнозирования температуры хладноломкости образцов или деталей с концентраторами напряжений предлагается выражение:
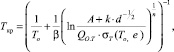(4)
где β, n – коэффициенты кривизны кривой зависимости предела текучести образцов на растяжение от температуры испытаний. Предлагаемую зависимость критической температуры хрупкости от размера зерна проверяли экспериментально. Было установлено, что увеличение размера зерна стали приводит к росту температуры хладноломкости. Сравнение расчетной и экспериментальной зависимости температуры хладноломкости от размера зерна указывает на возможность прогнозирования температуры хладноломкости стальных образцов по известному размеру ее зерна.
Разработанный подход к определению температуры хладноломкости образцов позволяет проводить расчет температуры хладноломкости деталей с учетом размера зерна стали. Для этого в формулу (4) вводится значение QО.Т определенное с помощью метода конечных элементов.
Таким образом, критическая температура хрупкости стального образца или детали с концентратором напряжений может быть оценена по заданному размеру зерна с одновременным учетом скорости, способа нагружения и геометрии образца или детали и концентраторов напряжений.