Вибрация в современной технике, на транспорте и в энергетике является одним из самых вредных динамических эффектов. Причиной вибрации является дисбаланс вращающихся масс. Задача эффективного устранения вибрации является одной из главных задач повышения качества выпускаемых машин и оборудования как на стадии их производства, так и в процессе их эксплуатации. С другой стороны в последние годы находят все более широкое практическое применение механизмы, принцип работы которых основан на преобразовании энергии центробежных сил инерции вращающихся дебалансов в вибрацию для технологических процессов. В этой связи исследования динамики вращающихся дебалансных масс для различных кинематических схем механизмов является весьма актуальной и имеет большое значение для инженерных расчетов инерционных приводов.
Цель исследования. Теоретические основы широко применяемой в строительстве вибрационной техники, касающиеся вопросов линейных и нелинейных задач динамики центробежных вибровозбудителей, динамики ударно-вибрационного привода и вибрационных процессов, энергетических соотношений при колебаниях и динамического управления колебаниями разработаны достаточно полно [1].
Вместе с тем в последние годы во всем мире ведутся разработки инерционных приводов для энергетических и силовых машин. Принцип этих приводов основан также на использовании энергии центробежных сил инерции. Например, известен силовой привод, основанный на вращении дебалансов, которые за счет центробежных сил инерции создают вращательные колебания на платформе. Эти колебания посредствам обгонных муфт передаются в виде вращательного движения генератору тока [2]. Известен также способ преобразования энергии центробежных сил инерции [5] путем создания центробежных сил инерции эксцентрических масс (дебалансов) установленных в платформе на сателлитах, которые вращают платформу, обкатывая центральное колесо, на котором создаются крутильные колебания.
Теоретические основы работы этих механизмов [2, 5] разработаны еще не достаточно. Это сдерживает развитие этого направления альтернативной энергетики.
В этой связи проведем анализ одной из возможных кинематических схем колесного планетарного механизма с дебалансной массой, математическая модель которого представлена на рисунке.
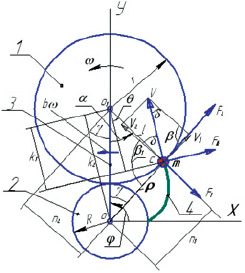
Математическая модель инерционного механизма
Механизм состоит из колеса 1 радиусом r, который обкатывается с угловой скоростью без скольжения по заторможенному центральному колесу 2 радиусом Rв горизонтальной плоскости (для исключения влияния сил тяжести) при помощи водилы 3, который будет вращаться с некоторой угловой скоростью, которая определяется геометрическим соотношением радиусов колес. На колесе 1 на расстоянии l от центра его вращения размещена масса m. Для нашего примера l = r. При этом центр массы m будет перемещаться по эпициклоиде 4. Параметрическое уравнение этой эпициклоиды в зависимости от соотношения радиусов колес b = r/R (модуль эпициклоиды)будет иметь вид [4, с. 75]
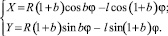 (1)
(1)
Модуль эпициклоиды b определяет её форму, соотношение между углами поворота и угловыми скоростями колеса 1 и водилы 3. Характер эпициклоиды является циклическим и в зависимости от модуля изменяется частота этих циклов.
Радиус вектор ρ центра смассы m (расстояние от центра масс с(m) до оси О вращения водилы 3) определяется из системы уравнений (1) и его зависимость от угла поворота φ и геометрических размеров будет иметь вид
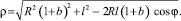 (2)
(2)
Здесь при расчетах следует учитывать, что φ = bα.
В процессе движения на массу m будут действовать центробежные силы инерции:
F1 = mlω2 – от вращения вокруг оси О1, (3)
F2 = mρb2ω2 – от вращения вокруг оси О, (4)
Fк = 2mVbω –сила Кориолиса, (5)
где V – скорость точки с(m). Эта скорость будет результирующей тангенциальных скоростей V1 = lω и V2 = ρbω и по модулю будет равна
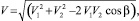 (6)
(6)
где β = π – β1. Подставляя значения тангенциальных скоростей и угла β в (4), получим
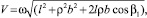 (7)
(7)
где 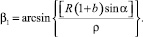 (8)
(8)
Выражения (5) и (6) позволяют определить скорость движения центра масс с (m)и силу инерции Кориолиса. Зная модули сил инерции и их направления, определим суммарный момент этих сил M1 относительно оси О1, вокруг которой вращается колесо 1, и суммарный момент М относительно оси О, вокруг которой вращается водила 3. Принимая знаки составляющих моментов положительными – при совпадении их направления с направлением угловой скорости этих звеньев, и при несовпадении –отрицательными, получим
M1 = F2∙n2 + Fкk1, (9)
M = –F1n1 – F2n2 – Fкk2. (10)
Здесь плечи воздействия инерционных сил определяются из геометрических соотношений и равны
n1 = R(1 + b)∙sinα; (11)
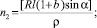 (12)
(12)
k1 = l∙sin (β1 – δ), (13)
где 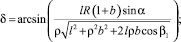
k2 = R(1 + b)∙sin (α + β1 – δ). (14)
Подставляя в (9) и (10) выражения сил инерции и их плеч, получим
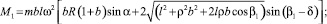 (15)
(15)
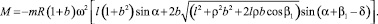 (16)
(16)
Полученные выражения позволяют определить характер изменения крутящих моментов возникающих от действия центробежных сил инерции в зависимости от скоростных и геометрических параметров механизма, а также от величины массы и расположения центра масс дебаланса.
Поскольку представленная схема механизма допускает множество вариантов компоновки привода, выражения (15) и (16) необходимы для составления дифференциальных уравнений движения конкретных механизмов на представленной базе.
Зная значения крутящих моментов (15) и (16), определим мощности, которые создают центробежные силы инерции на колесе 1 и водиле 3
N1 = M1ω; (17)
N = Mbω. (18)
Следует отметить, что из-за циклического характера изменения центробежных сил инерции и, соответственно крутящих моментов и мощности, эти силовые факторы будут в определенных зонах циклов создавать сопротивление приводу, а в других – будут разгружать привод.
Для анализа влияния центробежных сил инерции на циркуляцию мощности и резонансные процессы важно знать степень изменения угловой скорости вращения. Это связано с тем, что мощность вращательных приводов определяется произведением крутящего момента на угловую скорость.
При этом следует отметить, что для данного механизма в силу закона сохранения момента количества движения (Jω = const, где J – суммарный момент инерции системы) угловые скорости вращения подвижных звеньев не будут постоянными из-за изменения момента инерции системы. Суммарный момент инерции механизма (рисунок) относительно центра вращения О можно определить по известным зависимостям
J = ∑Jn + mρ2, (19)
где ∑Jn – суммарный момент инерции составляющих звеньев механизма с постоянным моментов инерции; mρ2 – приведенный момент инерции центра масс дебаланса, который изменяется в зависимости от значения ρ.
Из выражения (2)видно, что радиус вектор центра масс дебаланса изменяется в пределах (R + r – l) < ρ < (R + r + l), что позволяет определить минимальное и максимальное значение суммарного момента инерции. С учетом соотношения b = r/R получим
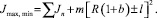 (20)
(20)
Таким образом, в соответствии с законом сохранения момента количества движения, угловая скорость в положении механизма с минимальным моментом инерции будет максимальна и, наоборот – в положении механизма с максимальным моментом инерции угловая скорость будет минимальна, то есть Jmaxωmin = Jminωmax. Из этого выражения, учитывая (20), определим максимальную угловую скорость
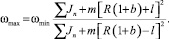 (21)
(21)
Это означает, что угловая скорость в процессе движения механизма в каждом цикле эпициклоиды будет импульсно меняться от максимального значения до минимального и обратно. Соответственно будет импульсно изменяться кинетическая энергия механизма. Определим кинетические энергии механизма T1 в положении механизма с максимальным радиус вектором ρ и T2 в положении механизма с минимальным радиус вектором ρ, которые по известным зависимостям можно записать в виде
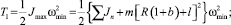 (22)
(22)
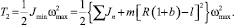 (23)
(23)
Подставим в выражение (23) значение (21) и, учитывая зависимость (22) получим
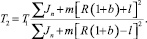 (24)
(24)
Выражение (24) показывает степень изменения кинетической энергии механизма при переходе его из положения с максимальным радиус вектором ρ в положение с минимальным радиус вектором ρ. Для обеспечения этого прироста кинетической энергии необходимо создать импульсный привод механизма, который необходим для преодоления центробежных сил инерции в интервале указанного перехода.
Полученные аналитические зависимости позволяют проводить инженерные расчеты крутящих моментов и мощности создаваемых центробежными силами инерции эксцентрических масс в зависимости от их значений, скорости вращения и геометрических параметров механизма для оценки мощности привода и степени вибрации. Эти зависимости также применимы для анализа дифференциальных уравнений движения конкретных колесных механизмов в зависимости от системы привода и компоновки. Также показана техническая особенность рассмотренного механизма к циклическому изменению кинетической энергии.
Заключение
Указанная техническая особенность реализована в способе преобразования центробежных сил инерции [3], имеющим НОУ-ХАУ конструкторского исполнения. В настоящее время выполняются работы по экспериментальным исследованиям лабораторных образцов реализующих указанный способ преобразования центробежных сил инерции. Результаты этих исследований и детальный анализ полученных аналитических зависимостей будут представлены в следующих публикациях.



