Особенность работы комбинированных машин состоит в том, что в процессе выполнения рабочего процесса они получают неравномерную нагрузку от рельефа, вращающихся массивных неуравновешенных роторов, тракторного двигателя и др. Изучение факторов, влияющих на устойчивость хода комбинированных агрегатов, позволяет разработать и установить технические приемы повышения качества функционирования современных почвообрабатывающих и посевных машин [1, 2].
Практика эксплуатации машин и теоретические исследования показывают, что давление на опоры снижаются при уменьшении весовых характеристик агрегата и симметричной установки основных рабочих органов. Расчет устойчивости хода определяется параметрами равномерности глубины обработки почвы по ширине и прямолинейности движения агрегата вдоль линии тяги, виртуальных перемещений. Положение центра тяжести агрегата в пространстве в любой момент времени определяется тремя перемещениями вдоль оси координат ОХ, ОY, ОZ и тремя поворотами вокруг этих же осей. Для определения равномерности хода рабочих органов по глубине рассмотрим устойчивость хода агрегата в продольно-вертикальной плоскости. Исходя из агротехнических требований, глубина хода h рабочих органов имеет допустимые отклонения ±Dh.
Комбинированные агрегаты включают лапы с жестким или шарнирным креплением стоек на раме, ротационные катки на шарнирной подвеске с автономным копированием рельефа, выравнивающие устройства и др. Они находятся под воздействием приведенной силы сопротивления почвы R, которую разложим на горизонтальную и вертикальную реакции Rx и Ry, вес рабочего органа G = mg и добавочный конструктивный вес агрегата Qa, приходящийся на один рабочий орган, реакции сил тяги в шарнирах, которую разложим на две составляющие ХА и YA.
Силы реакции почвы Rx и Ry меняются в зависимости от влажности переменной плотности почвы, остальные силы являются постоянными, либо они изменяются в малых пределах. Закономерности изменения возмущающего момента на устойчивость хода рабочих органов можно установить по переменному углу q.
Составим дифференциальное уравнение движения агрегата, воспользовавшись уравнением Лагранжа второго рода:
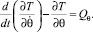
Проекции скорости перемещения центра масс на оси координат определим из уравнений:
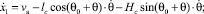
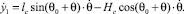
Значения кинетической энергии Т найдем из уравнения Штейнера:
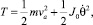
где m – масса системы; va – скорость центра масс агрегата; J0 – момент инерции системы относительно оси, проходящей через центр тяжести перпендикулярно к плоскости рамы и линии движения агрегата; Qq – обобщенная сила.
Уравнение Лагранжа можно записать через параметры динамической системы:
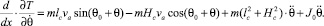
Тогда
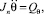
где 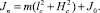
В уравнении виртуальной работы действующих на систему сил, коэффициент при виртуальном перемещении является обобщенной силой.
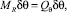
где MR – суммарный момент всех сил, приложенных к раме агрегата относительно точек крепления рабочих органов.
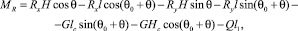
где l – длина шарнирной рамы для крепления рабочих органов к общей раме агрегата; lс – расстояние от точки прицепа до центра тяжести секции рабочих органов; l1 – расстояние от точки прицепа агрегата до точки приложения дополнительной нагрузки; H – высота рамы для крепления рабочих органов; Hс – расстояние от рамы агрегата до центра тяжести рабочих органов; Rx, Ry – соответственно горизонтальная и вертикальная сила сопротивления рабочих органов; G – вес рабочих органов; Q – дополнительная догрузка рабочих органов.
После преобразования синуса и косинуса двойного угла получим
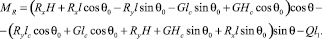
Отсюда
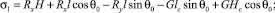
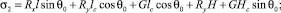
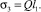
Заменяя алгебраические полиномы значениями s1, s2, s3, получим обобщенную силу:
MR = s1cosq – s2sinq – s3.
Интегрирование дает:
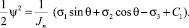
Время поворота рамы в виде
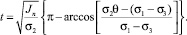
Значения угла q:
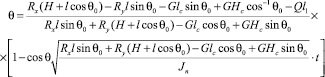
Это уравнение определяет закон изменения углов отклонения рам комбинированных агрегатов в зависимости от его размерных и режимных параметров. Подставляя значения параметров в это уравнение, можно определить их влияние на устойчивость хода агрегата. Для различных комбинированных машин их продольная база изменяется от 3 до 6 м. В равных условиях на качество копирования рельефа влияет, прежде всего, момент инерции агрегата, т. е. при увеличении продольной базы агрегата момент инерции возрастает пропорционально квадрату радиуса инерции. При этом угловые ускорения рамы уменьшаются обратно пропорционально моменту инерции агрегата относительно оси, перпендикулярной линии тяги трактора.
Расчет параметров силовых нагрузок на рабочие органы и рамы определяется по удельному сопротивлению почвы и внешним силам, действующим на агрегат.



