Для моделирования вероятных конфигураций межфазных границ на поверхности композиционных материалов может быть использован метод итерации видоизмененных кривых Коха (меандров) на определенных сетках Кеплера, которые включают в себя тетрагоны {4} (т.е. квадраты) в виде тел (например, сетки Кеплера 4444, 488, 46.12 или сетка Кеплера-Шубникова 44) [1]. В этом случае генерируется информация о вероятном квазифрактальном характере межфазных границ и их относительной поверхностной концентрации в виде характеристик предфракталов на совокупности простых геометрических 2D-фигур, которые можно рассматривать в качестве сечений 3D-многогранников – простейших аппроксимантов формы микрочастиц фаз [2]. Ранее были опубликованы методики вывода фрактальных структур в 2D-пространстве [3, 4] и мультифрактальных множеств кривых на периметрах 2D-сеток [5, 6].

Прямоугольный генератор-меандр К(8/4) является первым членом двух гомологических рядов меандров вида K((6n + 2)/(2n + 2)) и К((10n – 2)/(2n + 2)), где n = 1,2,3…∞ (рис. 1).

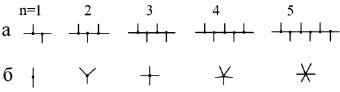
Рис. 1. Изображения первых четырех членов гомологических рядов меандров K((6n + 2)/(2n + 2)) и К((10n-2)/(2n + 2)) (б)

При многократном действии генераторов K((6n + 2)/(2n + 2)) на периметр ячейки квадратной сетки Кеплера-Шубникова 44 (где символ  означает лакуну) с топологией тетрагонов 4(2) из {4}-тел и {4}-лакун формируются упорядоченные в 2D пространстве одинаковые симметричные фигуры в соотношении 1:1 и с топологией связности с эквивалентными фигурами 4(2) (рис. 2).

На квадратной сетке Кеплера 4444 формируется упорядоченное множество предфрактальных кривых, которые обертывают одинаковым образом ориентированные и идентичные по симметрии фигуры (рис. 2). По мере увеличения порядкового номера гомолога закономерно увеличивается число вершин упорядоченных на сетке псевдоквадратных снежинок Коха. С каждым i-м поколением длина Li замкнутой фрактальной кривой в ряду

K((6n + 2)/(2n + 2))

возрастает по закону

Li = (3n + 1)Li-1/(n + 1)

(где n – порядковый номер члена ряда), а размерность ее

D = ln(6n + 2)/ln(2n + 2)

при n → ∞ закономерно уменьшается от 1,500 до 1,001.

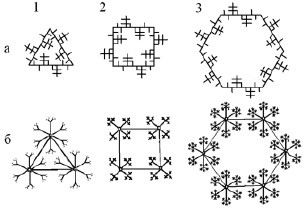
Рис. 2. Изображения прямоугольного генератора К(8/4), схемы его действия внутри 4-лакуны сетки Кеплера-Шубникова 44 и фрагмента лакунарного предфрактала 2-го поколения

При многократном действии генераторов К((10n – 2)/(2n + 2)) на периметр ячейки квадратной сетки Кеплера-Шубникова 44 с топологией тетрагонов не выше 4(2) из {4}-тел и {4}-лакун также формируются упорядоченные в 2D-пространстве одинаковые симметричные фигуры в соотношении 1:1. На квадратной сетке Кеплера 4444 формируется упорядоченное множество предфрактальных кривых, которые обертывают одинаковые по конфигурации, ориентации и симметрии фигуры. В гомологическом ряду генераторов

К((10n – 2)/(2n + 2))

закономерно увеличивается число вершин псевдоквадратных снежинок Коха, а с каждым i-м поколением длина замкнутой фрактальной кривой возрастает по закону

Li = (5n – 1)Li-1/(n + 1).

Фрактальная размерность кривой

D = ln(10n – 2)/ln(2n + 2)

принимает максимальное значение 1,613 при n = 2, а затем при n → ∞ закономерно уменьшается также до значения 1,001.

Полученные результаты моделирования вероятных конфигураций межфазных границ могут быть использованы при определении параметров синергической модели «концентрационной волны» [7] для расчета трибологических свойств поверхности композиционных покрытий.