В учебных исследованиях предпринято более глубокое (в сравнении с институтской программой) изучение закона всемирного тяготения, по которому, как известно, имеется много нерешенных вопросов, вызывающих большой интерес к проблеме. В исследованиях принимали участие студенты В.А. Арефьева и В.В. Трутнева.
Понять закон тяготения современникам Ньютона было нелегко. Например, Лейбниц писал Гюйгенсу: «Я не понимаю, как Ньютон представляет себе тяжесть или притяжение. По его мнению, по-видимому, это некое необъяснимое нематериальное качество». Гюйгенс, в свою очередь, отвечал Лейбницу: «Что касается причины приливов, которую даёт Ньютон, то она меня не удовлетворяет нисколько, как и все другие его теории, которые он строит на своём принципе притяжения, кажущемся мне нелепым» [1].
В настоящее время в некоторых учебниках для средней школы утверждается, что закон всемирного тяготения установлен Ньютоном на основе рассмотрения взаимодействия Луны и Земли. Указывается, что центростремительное ускорение Луны в 3600 или 602 раз меньше, чем ускорение у поверхности Земли. В то же время радиус Земного шара в 60 раз меньше, чем расстояние от Земли до Луны. Отсюда Ньютон заключает, что сила притяжения обратно пропорциональна квадрату расстояния между взаимодействующими телами. Однако Ньютон в год открытия (1667) не мог использовать данный подход, т.к. сначала надо было знать закон взаимодействия между точечными телами, чтобы доказать, что сила взаимодействия между шарообразными телами (Землей и Луной) может быть заменена на силу взаимодействия между такими же по массе телами, расположенными в центре шаров. Для вычисления силы взаимодействия между протяженными (не точечными) телами, в том числе и шарообразными, их следует «разбить» на элементарные массы, чтобы их можно было считать материальными точками, посчитать по закону всемирного тяготения силы притяжения между всеми элементами, а затем геометрически их сложить (проинтегрировать), что является довольно сложной математической задачей [2] и впервые было выполнено, по-видимому, самим Ньютоном, а затем английским физиком Г. Кавендишем в 1789 г., который экспериментально доказал закон всемирного тяготения для земных тел и определил экспериментально числовое значение гравитационной постоянной. Здесь тоже возникает вопрос: были ли материалы шаров, которые использовал Г. Кавендиш абсолютно не магнитными (не диамагнитными и не парамагнитными), т.е. насколько отсутствовало влияние магнитного поля Земли и намагниченности шаров на их взаимодействие?
Для доказательства закона всемирного тяготения Ньютон использовал третий закон Кеплера [1, 2], согласно которому квадраты периодов обращения (Т) планет вокруг Солнца относятся как кубы больших полуосей их орбит (R) или, для одной планеты:
R3 = kT2. (1)
Здесь k - коэффициент пропорциональности. На наш взгляд рассуждения Ньютона могли сводиться к следующему. Центростремительная сила (Fц), действующая на эту планету массой (m), равна силе тяготения (Fт):
Fц = Fт.
т.е. mω2R = Fт или m(2π/T)2R = Fт тогда с учётом (1):
Fт = k4π2m/R2. (2)
Вводя в уравнение (2) пропорциональность массе Солнца (М) и гравитационную постоянную (G), он получил:
F = G(mM/R2). (3)
Далее Ньютон уточнил закон Кеплера, введя в него массы вращающихся космических тел. В настоящее время подобная задача есть в КИМах ЕГЭ. В ней рассматривается движение двойной звезды. Обозначения - на рис. 1. На основе равенства центростремительной силы и силы тяготения для каждой из звёзд (или планет типа Земля-Луна; обозначения на рисунке) запишем:
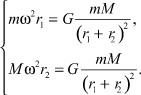
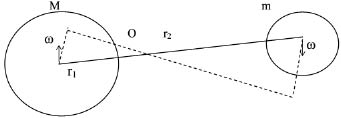
Рис 1
После сложения уравнений и замены ω = 2π/Т, получим:
![]()
учтем здесь r1 + r2 = R, тогда 4πR3 = G(m + M)T2. Или для двух таких систем
![]() . (4)
. (4)
Это и есть уточненный Ньютоном третий закон Кеплера.
Годом открытия закона всемирного тяготения является 1667 г. Однако в это время Ньютону было всего 24 года и интегральное исчисление им еще не было создано. Поэтому аналитически доказать закон всемирного тяготения для шарообразных тел он еще не мог. И лишь в 1687 году в «Математических началах натуральной философии» [3] он впервые строго доказал его, опираясь на созданные им математические методы, составившие основу дифференциального и интегрального исчисления. Используя закон всемирного тяготения и сформулированные им понятия массы и силы, Ньютон распространил его на взаимодействие Земли и Луны, Земли и тел на её поверхности, определил массы планет и Солнца в единицах массы Земли, объяснил возникновение приливов и отливов. Ньютон показал, что полученные им законы движения под действием тяготения имеют более общий характер; законы же Кеплера являются частным случаем этих более общих законов [1].
На первом этапе исследований с целью проверки справедливости замены в законе всемирного тяготения шарообразного тела (Ш) на точечное тело, помещенное в центр этого шара, при его взаимодействии с телом (Т) небольшого размера вблизи этого шарообразного тела мы провели расчеты, как бы не зная интегрального исчисления, т.е. возможно повторили расчеты И. Ньютона. Шарообразное тело (Ш) мы разделили множеством плоскостей (см. рис. 2) в трех взаимно перпендикулярных направлениях. В результате образовались элементы кубической формы, а на поверхности шара - усеченной кубической. Тело (Т) имело кубическую форму и такой же размер, как у каждого кубического элемента шара. Тело отстояло недалеко от поверхности шара (на расстоянии длины двух ребер кубического элемента). Кубические элементы и тело мы посчитали материальными точками единичной массы, расположив эти точки в геометрическом центре фигур. Между этими точками отсчитывали расстояние для расчета сил взаимодействия по закону всемирного тяготения. Массу тел усеченной формы (у поверхности шара) уменьшали в сравнении с единичной массой пропорционально уменьшению объема, а центр масс определяли как центр объёма фигур, и так же рассчитывали силу взаимодействия. Результатом исследований считали геометрическую сумму (Fc) сил взаимодействия каждого элемента шара (Ш) и тела (Т). Результатом явилось значение силы в условных единицах Fc = 0,080996. Сила взаимодействия между центром шара и центром тела Fц = 0,081204. Из этих данных относительное отклонение значений сил Fc и Fц от среднего значения составляет 0,13 %. Таким образом, при рассмотрении взаимодействия шара и находящегося вблизи него тела, шар вполне можно заменить на точечное тело, помещенное в центр шара и имеющее массу шара, т.е. Fc = Fц.
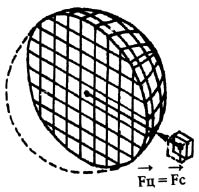
Рис. 2
Такие вычисления являются весьма трудоемкими и нашим студентам, участникам настоящих исследований, потребовалось около 20 часов, а с учетом уточняющих повторных вычислений преподавателем - еще больше. Такие вычисления с помощью компьютера проводятся за долю секунды (задания в программе MS Excel компьютеру пишутся дольше). Что было предпринято нами в последующих исследованиях (ч. II). Вероятно, Ньютон также проводил подобные вычисления - во все времена ученые много считали. Подход Ньютона был распространен на электрическое (закон Кулона, теорема Остроградского-Гаусса) и магнитное (закон Био-Саварра-Лапласа) поля.
Догадка и последующее доказательство Ньютона по замене шара на точечное тело, на наш взгляд, само является замечательным открытием, которое предопределило создание дифференциального и интегрального исчисления.
Далее легко выполнить полученные доказательства для двух шарообразных тел, так же разбив их на точеные элементы. Тогда для каждого точечного элемента второго шара первый шар можно заменить первым точечным телом. А затем второй шар, рассматривая взаимодействие его элементов с первым точечным телом, так же можно заменить вторым точечным телом.
Специально следует отметить, что со времён Ньютона и до настоящего времени окончательно не установлена скорость распространения гравитации. Согласно Лапласу [1], скорость передачи притяжения можно определить по вековому ускорению движения Луны. По этим данным, притяжение должно было бы передаваться со скоростью, по крайней мере, в пятьсот миллионов раз превосходящей скорость света. Поэтому, не опасаясь какой-либо «заметной погрешности, мы можем принять передачу тяготения за мгновенную» [1]. До настоящих дней физическая сторона природы тяготения осталась столь же неясной, как и была. В общей теории относительности Эйнштейна тяготение может распространяться от одного тела к другому со скоростью света посредством волн гравитации. Попытки их обнаружить экспериментально, начатые в США и повторившиеся во всём мире вплоть до последнего времени к успеху не привели, гравитоны (носители гравитационного поля) и гравитационные волны не обнаружены. Определение скорости распространения гравитации является одной из важных задач, которую должна решить современная наука.
Список литературы
- Воронцов - Вельяминов Б.А. Лаплас. - 2-е изд., доп. и перераб. - М.: Наука, 1985. - 288 с.
- Трофимова Т.И. Курс физики: учеб. пособие для вузов. - 15 изд. - М.: Академия, 2007. - 560 с.
- Рябов Ю.А. Закон всемирного тяготения // БСЭ. - http://bse.sci-lib.com/article082932.html.



