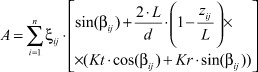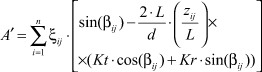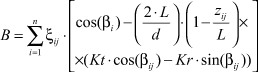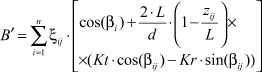В различных отраслях промышленности все более широкое применение находят несоосные винтовые механизмы, в том числе роликовые винтовые передачи (РВП), имеющие преимущество перед традиционными шариковыми винтовыми передачами по целому ряду параметров: редукции, коэффициенту полезного действия, точности, грузоподъемности и т.д. [1].
Детали НВМ в процессе эксплуатации подвергаются нестационарному повторно-переменному нагружению и выходят из строя в результате усталостного разрушения. С целью повышения долговечности сопрягаемые детали НВМ подвергают упрочняющей обработке. Для технологического обеспечения долговечности и качества передачи необходима информация о напряженном состоянии деталей, формирующемся в процессе эксплуатации НВМ [3].
Задача определения напряженного состояния сводится к расчету главных (экстремальных) напряжений от всех действующих силовых факторов в любой точке детали в произвольный момент времени [2]. Данные о значениях экстремальных напряжений в локальной области несущей детали НВМ в тот или иной момент времени являются основой расчета параметров спектра нагружения и глубины наиболее нагруженного несущего слоя. Сведения о спектре нагружения несущей поверхности дают возможность прогнозировать ее долговечность. Знание глубины несущего слоя позволяет предъявить научно обоснованные требования к величине, знаку и градиенту изменения технологических остаточных напряжений. Это создает предпосылки выбора рационального технологического маршрута и режимов обработки несущей поверхности.
Наибольший интерес представляет расчет напряженного состояния наиболее сложной в технологическом отношении детали НВМ-ходового винта.
Напряженное состояние ходового винта формируется в результате силового взаимодействия сопрягаемых поверхностей винта и гайки (для простого НВМ) или винта и роликов (для РВП). В связи с фрикционным характером передачи движения в НВМ при рассмотрении силового взаимодействия контактирующих поверхностей необходимо учитывать суммарное влияние сил давления и трения, что не позволяет ограничиваться при решении формулами Герца.
Предлагается следующая методика поэтапного расчета главных напряжений:
- определение главных напряжений в каждой точке тела винта, вызываемых действием всех силовых факторов;
- учет возрастания величины главных напряжений в местах их концентрации - у основания винтового зуба;
- расчет главных контактных напряжений в поверхностном слое;
- оценка действующих полей напряжений в теле и на поверхности винта с учетом величины и знака технологических остаточных напряжений.
Ниже рассмотрена методика расчета главных напряжений, формирующихся в результате действия всех силовых факторов при эксплуатации РВП, являющейся наиболее общим случаем НВМ.
При расчете главных напряжений ходовой винт допустимо моделировать брусом круглого сечения с закрепленными в опорах концами. Рассматривается плоское напряженное состояние винта. Определяются главные напряжения, формирующиеся в результате взаимодействия полей напряжений изгиба, кручения, растяжения, сжатия и сдвига. Главные напряжения в любой точке винта можно определить, подставляя приведенные в таблице аналитические выражения в известные формулы [2]:
(1)
(2)
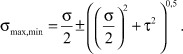(3)
Качественную оценку напряженного состояния, выявление характера зависимости σmax, min от переменных величин вне связи с конкретными конструктивными параметрами удобно производить, оперируя безразмерными коэффициентами, диапазон изменения которых заранее известен: r = 2ρ/d; Kd = L/d; Kz = z/L; Kzij = zij/L. При этом значения r, Kz, Kzij лежат в диапазоне от 0 до 1 включительно, а Kd много больше единицы. Выполнив преобразования, переходя в формулах (1), (2) к безразмерным коэффициентам, получим:
при z ≤ zi1:
(4)
(5)
при 
:
(6)
(7)
при 
, 
:
(8)
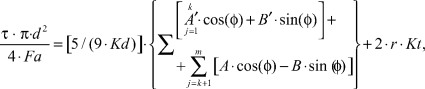(9)
где zi1 - линейная координата первой точки контакта винта с i-м роликом; S - шаг резьбы ролика; К - число заходов резьбы ролика.
В несоосной винтовой паре при постоянной осевой нагрузке на винт, составляющие ее переменны [1]. Входящие в формулы (4)-(9) и таблицу радиальная Fr и тангенциальная Ft составляющие нагрузки в контакте сопрягаемых деталей РВП могут быть выражены через осевую Fa составляющую векторной суммы сил давления и трения: Fr = Fa⋅Kr; Ft = Fa⋅Kt. Проведенные исследования показали, что Kr и Kt принимают значения в диапазонах: 0,45 ≤ Kr ≤ 1,17; 0 ≤ Kt ≤ 0,57, причем наибольшим значениям Kr соответствуют средние и малые значения Kt, а наибольшим Kt - средние и малые Kr. Наибольшая величина главных напряжений соответствует максимальным значениям Kr и Kt, поэтому для расчетов целесообразно принять Kr = 1,2 и Kt = 0,6.
В формулах использованы следующие обозначения: L - длина ходового винта; d - диаметр винта; 
- доля нагрузки, воспринимаемая j-й точкой контакта винта с i-м роликом; n - количество роликов; m - количество точек контакта одного ролика с винтом; ρ, Φ, z - полярные и линейная координаты точки, в которой определяются напряжения; ρ = d/2, 
, zij - полярные и линейная координаты точек контакта винта с j-й точкой контакта винта с i-м роликом (точки приложения нагрузки). Нулевые точки для ρ находятся на оси вращения ходового винта, углы φ и βij отсчитываются от оси х против часовой стрелки, а z и zij - от левого торца винта.
Подставляя (4)-(9) в (3) и учитывая, что i = f(t), где t - время, можно получить формулы для определения главных напряжений от всех действующих силовых факторов в любой точке детали в произвольный момент времени.
Формулы для определения напряжений в ходовом винте от силовых факторов
|
При Z1 ≤ Z |
При Z1 > Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В результате численного эксперимента и анализа взаимного влияния φ, r, Kd, Kz, Kzij, Δβij, Δξi, Δξj, для 
установлено, что:
- зависимость Kσ от Kd мало отличается от линейной, чем больше величина Kd, тем большие значения принимает Kσ при прочих равных условиях;
- главные напряжения имеют максимум на поверхности винта и убывают линейно по направлению к оси вращения;
- величина погрешности положения роликов в диапазоне Δξi = 3 оказывает значительно меньшее влияние на величину Kσ, чем неравномерность распределения нагрузки по роликам Δξi;
- изменение неравномерности распределения нагрузки от нуля до максимума (для простого НВМ) приводит к увеличению Kσ в 2,3 раза.
Исследования показали, что для определения экстремальных значений напряжений на поверхности и на глубине 
винта несоосного винтового механизма с целью облегчения расчетов может быть предложена инженерная формула вида:
(8)
где Kξ - коэффициент, характеризующий неравномерность распределения нагрузки по роликам в РВП, изменяющийся в диапазоне 0,2-2,3.
Предложена методика расчета напряженного состояния ходовых винтов НВМ [4, 5]. В результате аналитического решения задачи получены выражения для определения главных напряжений в любой точке винта с координатами z, φ, ρ от действующих силовых факторов. Установлена степень влияния неравномерности распределения нагрузки по роликам, погрешности положения роликов, конструктивных параметров винта на величину главных напряжений. Предложена инженерная формула для расчета экстремальных эксплуатационных напряжений.
В экспериментальном исследовании применялась стандартная прямоугольная розетка датчиков для определения деформаций по трем направлениям. После определения деформаций перешли к компонентам напряженного состояния в упругой области, воспользовавшись законом Гука.
Образец изготовлен из стали, он имитировал ходовой винт НВМ. Для более точного определения напряжений нагрузку прикладывали ступенями.
Построены графики теоретических и экспериментальных данных по методу тензометрии. Расхождение между экспериментальными и теоретическими значениями главных и расчетных напряжений составляет не более 5 %. Незначительное расхождение между экспериментальными и теоретическими значениями главных напряжений позволяет считать разработанную методику достаточно точной и рекомендовать ее для расчета напряженного состояния ходовых винтов.
Список литературы
- Бушенин Д.В. Несоосные винтовые механизмы. - М.: Машиностроение, 1985. - 112 с.
- Бушенин Д.В., Киричек А.В., Лодыгина Н.Д. Исследование и расчет напряжений и деформаций ходового винта РВП // Зубчатые передачи - 96. Проблема обеспечения надежности и качества зубчатых передач: Тез. Междунар. научн.-практ. конф. - СПб., 1996. - С. 26.
- Киричек А.В. Повышение долговечности роликовых винтовых передач технологическими методами // Ресурсо- и энергосберегающие технологии в промышленности: материалы Междунар. научн.-техн. конф., Одесса, 4-6 сентября 1996. - Одесса: УДЭНТЗ, 1996. - С. 69-70.
- Лодыгина Н.Д., Зелинский В.В., Курасов Е.В. Напряженное состояние ходового винта при неравномерном распределении нагрузки в РВП // Успехи современного естествознания. - 2007. - № 2. - С. 52-52.
- Шарапов Р.В., Лодыгина Н.Д. Расчет напряжений деталей несоосного винтового механизма // Фундаментальные исследования. - 2009. - № 5. - С. 70-71.