Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Динамическое поведение доменной структуры образцов железокремнистых сплавов, составляющий основу электротехнических материалов, в значительной мере определяет их магнитные характеристики.

Интерес к изучению динамического поведения доменной структуры и его особенностях по сравнению с квазистатическим обусловлен широким применением этих магнитомягких материалов для изготовления магнитопроводов различных электротехнических агрегатов и устройств - трансформаторов, электрических машин, приборов, магнитных пускателей, контакторов, реле, дросселей и т.п. Учитывал, что уровень магнитных свойств этих материалов определяет качество, надежность и долговечность работы электротехнических агрегатов и устройств, то выяснение механизма формирования свойств таких материалов и путей их улучшения способствует повышению качества, надежности и долговечности работы электроэнергетических систем. Кроме того выяснение механизма формирования свойств материалов перспективно для создания систем связи и обработки информации.

К настоящему времени существует значительное число исследований. показывающих, что коэрцитивная сила зависит от химического состава включений, от их размера, от величины кристаллита и ориентации их намагниченности, от плотности дислокаций, а также от их структуры и характера распределений.

В частности, Виценой в 1955 г. предложена следующая зависимость коэрцитивной силы от плотности дислокаций [1].

           (1)

где Н_с - коэрцитивная сила; N - плотность дислокаций.

Однако предложенная Виценой формула далека от истины и даже по порядку величины не соответствует значению коэрцитивной силы.

Многочисленные испытания показывают, что величина коэрцитивной силы и максимальной магнитной проницаемости зависят не только от плотности дислокаций, но и одновременно от числа доменов и характера их взаимодействия.

Целью настоящей работы являлось исследование характера взаимодействия доменных границ с дислокациями и их количественное влияние на коэрцитивную силу и максимальную магнитную проницаемость. Практический интерес представляет определение зависимости скорости движения зародышей перемагничивания в материале от плотности распределения дислокаций и количественного содержания кремния.

Для расчета коэрцитивной силы, допустим, что в отсутствие внешнего поля под действием обменных сил каждый кристаллит намагничен до насыщения в одном из направлений легкого намагничивания. Рассмотрим процесс перемагничивания одного из кристаллитов в противоположном направлении. С этой целью начнем постепенно увеличивать внешнее поле. В микроскопическом объеме, примыкающем к границе кристаллита, происходит зарождение антифазного домена, отделенного от остальной части кристаллита стенкой. Для определенности рассмотрим 180-градусные доменные границы. Затем под влиянием того же внешнего поля процесс перемагничивания кристаллита начинается со смещения 180-градусных доменных границ. Последующее изменение его намагниченности будет происходить за счет развития и роста зародышей перемагничивания. Это обстоятельство и приводит к увеличению свободной энергии кристаллита. Как известно, если в общем виде внешнее поле Н направлено под углом 9 к вектору самопроизвольной намагниченности I_s, то изменение магнитной энергии для 180- градусной границы определяется следующим образом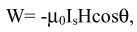[2]:

         (2)

где μ₀ - магнитная постоянная, μ₀ = 4π • 10^-7 Гн/м.

Допустим, что необходимо перемагнитить однодоменную частицу в направлении, противоположном тому, в котором она самопроизвольно намагничена при отсутствии внешнего магнитного поля, т.е. в формуле (2) положим, что θ=180 , тогда

W= μ₀ I_sH.           (3)

Взаимодействие между дислокациями и плоскими Блоховскими стенками определяется стохастической силой Пича-Колера. Давление, вызванное действием внешнего поля, можно определить по формуле [3]:

P=α • I_s •H,              (4)

где Р - давление на доменную границу;

α=2 для 180-градусной доменной границы,

α=1 для 90-градусной доменной границы.

С увеличением напряженности магнитного поля стенка все больше смещается в одну сторону, причем объем стенки непрерывно увеличивается. Такое положение и приводит к увеличению свободной энергии кристаллита. При определенной напряженности магнитного поля стенка займет положение, при котором объем правового домена будет равен объему левого домена, следовательно, результирующая намагниченность кристаллита станет равной нулю. Эта напряженность магнитного поля в соответствии с определением и будет коэрцитивной силой.

Таким образом, доменная граница все больше и больше смещается в одну сторону с ростом зародыша и постепенным уничтожением существующего домена, что приводит к увеличению свободной энергии кристаллита по следующей формуле:

W • ΔV= μ₀ I_s • H_c •  ΔV.                (5)

Эксперименты показали, что уменьшение коэрцитивной силы коррелирует с уменьшением плотности дислокаций. Запишем уравнение для зависимости коэрцитивной силы от плотности дислокаций в логарифмической форме:

lnH_c = A + C₁ lnN / N_o,                       (6)

где А - постоянная величина;

С₁ - постоянная логарифмирования;

N - текущая плотность дислокаций;

N_o - максимальная плотность дислокаций.

Эксперименты показали, что чем выше концентрация доменов, тем меньше величина коэрцитивной силы. Запишем уравнение для зависимости коэрцетивной силы от концентрации доменов в логарифмической форме:

lnH_c = В - С₂ Іnn / n₀,                              (7)

где В - постоянная величина;

С₂ - постоянная логарифмирования;

n - текущая концентрация доменов;

n_o - максимальная концентрация дислокаций.

Сложим два уравнения (6) и (7):

2lnH_c=A+B+ C₁lnN/N_o - lnn/n_o                     (8)

Запишем полученную функцию в виде натуральной показательной функции:

                            (9)

Произведя потенцирование, найдем

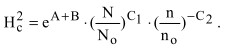               (10)

Извлекая квадратный корень, получим

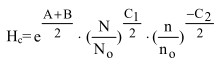                      (11)

Энергию, характеризующую взаимодействие доменной границы с дислокациями, по предложению автора можно определить по следующей формуле:

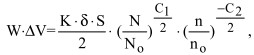               (12)

где К - константа магнитной анизотропии;

δ - толщина доменной стенки;

S - толщина прохождения доменной стенки;

Увеличение энергии на одну и ту же величину приведет к равенству выражений (5) и (12):

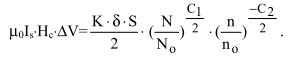             (13)

В выражении (13) предлагается рассматривать , где считаем  - объем кристаллита.

Из соотношения (13) определяем коэрцитивную силу:

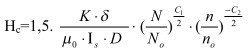    (14)

В качестве примера рассчитаем конкретные величины С₁ и С₂ из экспериментальных наблюдений. Для плотности дислокаций N=7-10¹⁰ м^-2 и концентрации доменов n=8·10⁵ м^-2 показатели степени равны С₁= -0,3 и С₂=4,5, а для плотности дислокаций N=2·10¹³ м^-2 и концентрации доменов n=9·10³ м^-2 - С₁=0,5 и С₂=3.

Эксперименты показали, что чем меньше плотность дислокаций, тем выше максимальная магнитная проницаемость. Запишем уравнение для зависимости максимальной магнитной проницаемости от плотности дислокаций в логарифмической форме:

lnμ = A_μ-C_1μ lnN/N_o,                        (15)

где A_μ - постоянная величина;

С_1μ - постоянная логарифмирования;

N - текущая плотность дислокаций;

N_o - максимальная плотность дислокаций.

Эксперименты показали, что повышение максимальной магнитной проницаемости коррелирует с повышением концентрации доменов. Запишем уравнение для зависимости максимальной магнитной проницаемости от концентрации доменов в логарифмической форме:

lnμ= В_μ+C_2μlnn/n_o,                        (16)

где В_μ- постоянная величина;

C_2μ- постоянная логарифмирования;

n - текущая концентрация доменов;

n_o - максимальная концентрация дислокаций.

Сложим два уравнения (15) и (16):

                          (17)

Запишем полученную функцию в виде натуральной показательной функции:

                     (18)

Произведя потенцирование, найдем

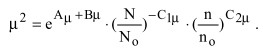        (19)

Извлекая квадратный корень, получим

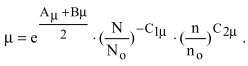. (20)

В ферромагнитных материалах максимальная магнитная проницаемость определяется из выражения [2]:

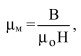                      (21)

где В - магнитная индукция.

Максимальная магнитная проницаемость является структурно чувствительной величиной, которая зависит от взаимодействия доменных границ с дислокациями. Поэтому с учетом этого для определения максимальной магнитной проницаемости автором была скорректирована формула следующим образом:

                    (22)

Для плотности дислокаций N=4 ·10¹⁰ м^-2 и концентрации доменов n=7·10⁵ м^-2 показатели степени равны C_1μ=1,5 и C_2μ=2,5, а для плотности дислокаций N=7 ·10¹³ м^-2 и концентрации доменов n=9 ·10³ м^-2 - C_1μ=40 и C_2μ=1,4.

Домен со своими стенками является совокупным материальным макроскопическим объектом, для которого можно применить формулу кинетической энергии:

E=mV²/2.        (23)

Из этой формулы можно примерно оценить скорость движения доменной границы:

                     (24)

где Е-энергия доменной границы (для железа Е≈5,35-10^-16 Дж);

m - эффективная масса 180-градусной доменной границы (для железа m≈ 3,7·10^-20 кг).

Полученные закономерности имеют теоретическое значение поскольку позволяют установить взаимосвязь редукционного структурного несовершенства ферромагнитных материалов с динамическими характеристиками процессов перемагничивания.

ВЫВОД

В результате исследования физических свойств сплавов, составляющих основу электротехнических материалов, теоретически определено, что магнитные свойства зависят от совместного взаимодействия доменной и дислокационной структур.

ЛИТЕРАТУРА

1. Vicena F. On the influence of dislocations on the coercive field of ferromagnetic / - «Chechosl. I. Phys.». 1955. V. 5, p. 480-485.
2. Мишин Д. Д. Магнитные материалы. - M.: Высшая школа, 1991. 384 с.
3. Pfeffer K.H. Pfys. sat. sol. 21. 857 (1967). V. 20-21.