Современный этап модернизации высшей технической школы России обусловливает поиск и разработку новых технологий обучения, адаптацию к учебному процессу инновационных технологий и методов обучения, обеспечивающих развитие познавательных, созидательных и творческих способностей студентов, соответствующих современным жизненным потребностям развитой личности.
Повышение качества подготовки инженеров по безопасности жизнедеятельности в техносфере достигается интенсивной прикладной математизацией содержания образования, использованием широкого спектра методов анализа технической информации, освоением информационных технологий и ресурсов. В связи с этим, значительное место в системе формирования у будущего выпускника профессиональной компетентности отводится дисциплинам, обладающим значительным научно-исследовательским потенциалом. Таковой является дисциплина «Надежность технических систем и техногенный риск», в которой изучаются инженерные методы исследования надежности технических систем и методы снижения риска. Содержание этой дисциплины в профессиональном плане направлено также для показа силы математических методов в инженерном приложении, представляет важную общенаучную составляющую в образовательной программе и является одним из основных компонентов подготовки компетентного инженера по безопасности жизнедеятельности в техносфере.
В интеллектуальном плане содержание этой дисциплины имеет большие возможности для развития логического мышления и технического воображения, ряда других интеллектуальных качеств, таких как готовность памяти, логико-модельное мышление, его самостоятельность и гибкость, способность к оценочным действиям, легкость генерирования идей и т.д.
Существенную проблему реализации сложного содержания представляет значительное несоответствие между объемом изучаемого материала и количеством часов, отводимых на его овладение. Также на качество усвоения знаний влияет сложность самого предмета, обусловленная высокой степенью его понятий, сложностью математического аппарата и введением элементов логического анализа, графологических структур. Следует заметить и тот факт, что у многих студентов недостаточно развиты умения самостоятельной работы и надлежащая учебная мотивация из-за отсутствия представления о важности математических приложений в инженерных дисциплинах.
Совершенствование преподавания этой дисциплины надлежит осуществлять в направлении раскрытия её статуса путем большей визуализации, а преподавание выстраивать так, чтобы преодолеть формализм знаний и барьеры понимания содержания, сформировать целостное представление о предмете.
Решение обозначенных выше задач возможно осуществить при условии интеграции в процесс обучения современных технологий обучения, усиливающих личностную направленность, дифференциацию и индивидуализацию, являющихся эффективным средством управления познавательной деятельностью студентов.
Цель исследования: конструирование обучающего модуля, как части содержания учебной дисциплины, позволяющего реализовать интеграцию различных форм учебной деятельности в рамках изучения содержания наиболее трудоемких разделов общеинженерных дисциплин, обеспечивающего высокую эффективность процесса формирования профессиональной компетенции.
Методы исследования
Отечественная и зарубежная практика показывает, что поставленной цели можно достигнуть, внедрив в учебный процесс технологии модульного обучения [2; 4; 5; 6], представляющие собой способ реализации заданного содержания обучения с помощью упорядоченной и целесообразной совокупности методов, средств и форм, направленных на формирование приемов и способов интеллектуальной деятельности. По оценкам исследователей (П.И. Третьяков, И.Б. Сенновский, П.А. Юцявичене и др.), модульное обучение позволяет сократить учебный курс дисциплины примерно на 30 % без ущерба для полноты изложения и глубины усвоения материала. Сжатие учебного материала происходит посредством укрупненного, системного его представления при первичном, промежуточном и конечном обобщении.
В рамках нашей работы, обучающий модуль - это логически завершенная форма части содержания учебной дисциплины, подкрепленная соответствующей информационной и методической поддержкой, формой контроля, включающая в себя целостный набор теоретических знаний, подлежащих изучению и овладению практическим опытом их применения путем решения практических задач с использованием компьютера как инструмента вычисления и средства обучения. При конструировании обучающего модуля мы в первую очередь исходили из того, что информационные технологии [3] и применение компьютерной поддержки значительно расширяет возможности процесса изучения сложных, математизированных предметов [1]. В частности, компьютерная поддержка обеспечивает численную обработку результатов экспериментальных исследований и сложных математических задач, связанных с проведением большого объема вычислений. В результате снижается утомляемость от выполнения рутинных вычислений, мотивируется познавательная деятельность обучающихся, учебный процесс становится высокопродуктивным и предоставляется возможность освоить большее содержание в рамках одной дисциплины. В свою очередь, продуктивная деятельность, направленная на получение личностно значимого результата (продукта деятельности, полученного самостоятельно), содержит достижение качественных сдвигов в понимании предмета, взаимообусловленное изменениями в структуре деятельности обучаемого.
Результаты исследования и их обсуждение
Модуль содержит познавательную (информационную, теоретическую) и учебно-профессиональную (практическую, творческую) части. Задача первой - формирование теоретических знаний, функции второй - формирование профессиональных умений и навыков на основе приобретенных знаний. Цели обучения формируются как результат деятельности студентов с точки зрения их продвижения и развития в процессе усвоения определенного опыта. Их определение предшествует отбору содержания тем и заданий.
Приведем описание практической части модуля. Она состоит из трех разделов, сконструированных идентично: методы расчета; типовые примеры и их решения; задачи различного уровня сложности; контрольные вопросы.
Первый раздел сконцентрирован на расчете количественных характеристик надежности. Включает типовые задачи расчета - задачи, которые встречаются при определении количественных характеристиках надежности по статистическим данным об отказах системы и при известном аналитическом выражении одной какой-либо характеристики. При решении задач первой группы используются статистические определения количественных характеристик надежности, при решении задач второй группы - вероятностные определения характеристик и аналитические зависимости между ними. Так как при анализе надежности объектом исследования являются случайные события и величины, то в качестве теоретических распределений наработки до отказа могут быть использованы любые применяемые в теории вероятностей непрерывные распределения случайных величин (задаются условиями задач): для дискретных величин - биноминальный закон, закон Пуассона; для непрерывных случайных величин - экспоненциальный закон, нормальный закон, гамма-распределение, закон Вейбулла, χ2 - распределение, логарифмически-нормальное распределение.
В сложных вычислениях используются табулированные значения различных функций. Вычисляемые значения графически представляются ступенчатыми кривыми или гистограммами, т. е. вычисления визуализируются и пользователю видно, каким образом изменяется надежность изделия при тех или иных условиях.
Второй раздел направлен на расчет характеристик надежности невосстанавливаемых изделий при различном соединении элементов: последовательном, параллельном, параллельно-последовательном.
Третий раздел посвящен расчету характеристик надежности невосстанавливаемых резервированных изделий. Расчеты осуществляются от простого расчета к более сложному. К простому - относится элементный расчет аппаратурной надежности простых изделий, нерезервированных, без учета восстановлений работоспособности при условии, что время работы до отказа подчинено экспоненциальному распределению. Более сложными расчетами являются вычисления надежности резервированных систем с использованием различных законов распределения времени работы; надежности резервированной системы в случае комбинаций отказов и внешних воздействий; надежности нагруженных элементов в случае статистически независимых и зависимых (множественных) отказов.
Выбор того или иного вида расчета определяется заданием исходя из индивидуальных возможностей обучающегося. На основании задания и последующего изучения работы устройства (по его техническому описанию) составляется алгоритм расчета надежности. На основе структурной схемы надежности составляется набор расчетных формул из числа приведенных в методических указаниях. Прежде чем применять эти формулы, необходимо предварительно внимательно изучить их существо и области использования.
Компьютерная поддержка представляет собой развитую информационную среду, моделирующую предметное содержание изучаемого материала, обеспечивающую расширение познавательной свободы обучаемого, и выступает как главный фактор обеспечения продуктивности модульной технологии обучения.
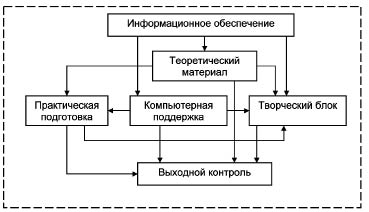
Структурная схема обучающего модуля
На рисунке представлена структурная схема обучающего модуля с компьютерной поддержкой и представлен блоками, имеющими следующее целевое назначение:
- блок «информационное обеспечение» раскрывает теоретическое содержание отдельной темы курса, реализуемое в ходе учебного процесса в форме лекций, практических, самостоятельной аудиторной и внеаудиторной курсовой работы студентов, контроля знаний. Позволяет управлять организацией и проведением целостного образовательного процесса во всех его
частях;
- блок «теоретический материал» предусматривает овладение системой новых научно-теоретических и специальных знаний;
- блок «практическая подготовка» реализует теоретические знания в форме практических работ, формирует умения и навыки учебной деятельности, обеспечивает возможность самостоятельно и целенаправленно использовать новые знания в практической работе;
- «творческий блок» (самостоятельная курсовая работа студентов) создает мотивацию к обучению, формирует гибкую систему обобщенных понятий, способствует интеграции полученных знаний в реальные условия исследовательской деятельности;
- блок «выходной контроль» позволяет на основе выходящей информации проанализировать эффективность образовательного процесса и внести соответствующие коррективы в его содержание и организацию;
- блок «компьютерная поддержка» учебного процесса в модуле представлена следующими направлениями: применение компьютера как средства вычисления; использование программирования, пакетов общего и специального назначения; применение компьютерных справочных материалов. Информатизация данного этапа позволяет освободить студента от необходимости производить сложные рутинные расчеты, вырабатывает у него навык работы с прикладными пакетами для проведения математических вычислений, предоставляет широкие возможность визуализации при помощи графиков и диаграмм проводимых вычислений.
Выводы. Наша практика показывает перспективность модульного обучения с компьютерной поддержкой, поскольку:
- изучается больший объем учебной информации за счет увеличения времени на практическую проработку отдельных теоретических тем, алгоритмизации учебной деятельности, согласованности и завершенности циклов познания;
- студент использует в обучении современные информационные технологии и средства, у него развиваются умения находить, преобразовывать и целесообразно использовать учебную информацию, он приобретает опыт самостоятельной познавательной деятельности и опыт самообразования;
- формирование положительной мотивации обучающихся ведет к активизации их познавательной деятельности, пониманию изучаемого предмета в противовес формальному «натаскиванию» на типовых задачах.
Список литературы
- Иванов С.Г. Компьютерная поддержка решения математических задач как средство организации продуктивной деятельности учащихся: дис. ... канд. пед. наук. - М., 2004. - 153 с.
- Гареев В.М., Руликов С.П., Дурпо Е.М. Принципы модульного обучения // Вестник высшей школы. - 1987. - №8. - С. 15-20.
- Новые педагогические и информационные технологии в системе образования: учеб. пособие / под ред. Е.С. Полат. - М.: Издательский центр «Академия», 2002. - 272 с.
- Третьяков П.И., Сенновский И.Б. Технология модульного обучения в школе: практико-ориентированная монография. - М.: Новая школа, 1997.- 352 с.
- Чошанов М.А. Гибкая технология проблемно-модульного обучения: метод. пособие. - М.: Народное образование, 1996. - 160 с.
- Юцявичене П.А. Теория и практика модульного обучения. - Каунас: Швиеса, 1988. - 272 с.



