Существующая в последние годы в вычислительных устройствах цифровой обработки сигналов (ЦОС) тенденция к распараллеливанию вычислений связана с непрерывным ростом требований к производительности вычислительных средств [1, 2]. В то же самое время это приводит к значительному усложнению структуры систем ЦОС. Таким образом, сложилось противоречие: с одной стороны, постоянный рост требований к скоростным характеристикам вычислительных устройств приводит к необходимости организации параллельных вычислений, а с другой стороны, при этом увеличивается частота возникновения отказов, и возрастает время простоя процессоров, вызванное трудностью отыскания и ликвидации неисправности. Наиболее перспективным путем разрешения данного противоречия является придание процессорам свойства отказоустойчивости [3].
Однако данная задача характеризуется повышенной сложностью решения. Поэтому целесообразно использовать системный подход к проектированию таких систем цифровой обработки сигналов. В этом случае методы и средства системного проектирования подготовят эффективную технологическую базу для достижения максимального уровня отказоустойчивости при обеспечении требуемых характеристик показателей качества функционирования устройства, таких как точность, скорость и достоверность обработки данных [4]. Опишем ключевые этапы выполняемых исследований и разработок в рамках системного проектирования.
В настоящее время качество реализации вычислений в конкретной предметной области во многом определяется выбранной математической моделью вычислений. Поэтому на первом этапе решается задача, связанная с выбором пространственно-временного распределения реализуемого вычислительного процесса we из множества 
структурированных алгоритмов его решения. В этом случае данная задача формулируется следующим образом:
(1)
Другими словами, необходимо определить единственное оптимальное, из совокупности возможных решений, при котором организация вычислений P(we) полностью соответствовала бы параллельно-конвейерной структуре вычислительного устройства P(D). Проведенные исследования показали целесообразность использования математической модели ЦОС, реализованной в кольце полиномов с использованием полиномиальной системы классов вычетов (ПСКВ) [1, 2].
Второй этап методики посвящен вопросам выбора системы оснований ПСКВ. Достижимая точность зависит от размерности обрабатываемых операндов, а так же разрядной сетки арифметических устройств. Чтобы избежать дополнительных ошибок, во время вычислений должна поддерживаться высокая точность. Если в качестве критерия оптимальности выбрать минимальные схемные затраты необходимы для обеспечения требуемой точности обработки данных, то математическая постановка задачи второго этапа примет вид
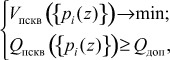(2)
где Vпскв - схемные затраты необходимые на реализацию процессора ПСКВ; Qпскв и Qдоп - точность обрабатываемых данных в модулярном коде и предельно допустимая точность; 
; pi(z) - минимальные многочлены расширенного поля Галуа GF(2v).
Решение многих прикладных задач осуществляется в реальном масштабе времени, что не позволяет возвращаться назад и исправлять появляющиеся ошибки. Поэтому необходимость своевременно обнаружения отказов, сбоев или других причин появления ошибочных результатов привела к необходимости введения контрольных оснований ПСКВ. Количество и величины контрольных модулей определяются согласно условиям, приведенных в [2]. В этом случае имеем следующую математическую постановку задачи
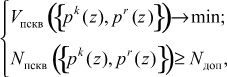(3)
где Vпскв - схемные затраты необходимые на реализацию процессора ПСКВ; Nпскв и Nдоп - количество отказов, парируемых при обрабатываемых данных в модулярном коде, и предельно допустимое значение.
Третий этап разработки устойчивых к отказам процессоров ПСКВ посвящен вопросам обоснования выбора алгоритма осуществляющего преобразование из позиционной системы счисления (ПСС) в модулярный код. На данном этапе наиболее важно собрать все имеющиеся данные о реализациях этой немодульной процедуры. По совокупности этих данных обосновывается математическая постановка задачи
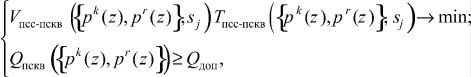(4)
где 
- j-й алгоритм прямого преобразования ПСС-ПСКВ; S - совокупность возможных алгоритмов прямого преобразования; Тпсс-пскв - временные затраты на реализацию немодульной процедуры преобразований ПСС-ПСКВ.
На четвертом этапе методики осуществляется выбор алгоритма обратного преобразования ПСКВ-ПСС и его схемной реализации. На данном этапе определяются особенности структуры и организации вычислительного устройства, выполняющего перевод из модулярного кода в позиционный. По этим данным исследуется и решается вопрос о целесообразности применения метода перевода из ПСКВ в ПСС с использованием китайской теоремы об остатках (КТО) или через смешанную систему счисления, проводится предварительный расчет аппаратурных затрат. В этом случае математическая постановка задачи имеет вид
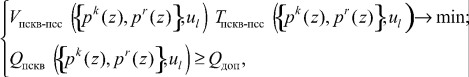(5)
где 
- l-й алгоритм обратного преобразования ПСКВ-ПСС; U - совокупность возможных алгоритмов прямого преобразования; Тпскв-псс - временные затраты на реализацию немодульной процедуры преобразований ПСКВ-ПСС.
На пятом этапе методики осуществляется анализ и выбор позиционной характеристики для выполнения контроля и коррекции ошибок. Исходя из условия, что ошибки вызванные отказами в вычислительных трактах процессора ПСКВ не перемещаются из одного основания в другое, то целесообразно контроль и коррекцию ошибок осуществлять параллельно с процедурой обратного преобразования ПСКВ-ПСС. Таким образом, математическая постановка задачи, решаемой на данном этапе, представляется
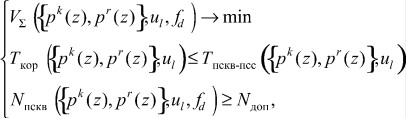(6)
где 
- суммарные схемные затраты на выполнение операции поиска и коррекции ошибки и обратного преобразования из ПСКВ-ПСС; Nдоп - предельно допустимое количество отказов; 
- количество парируемых отказов с использованием fd алгоритма вычисления позиционной характеристики; 
- совокупность возможных алгоритмов обнаружения и коррекции ошибок в кодах ПСКВ.
На последнем шаге системного проектирования осуществляется эффективности вычислительного устройства ЦОС. Для реализации данной процедуры был выбран показатель качества - вероятность безотказной работы P(t). При этом на ряд показателей качества функционирования устройства, таких как точность и время обработки данных, накладываются ограничения. Математическая постановка задачи данного этапа имеет вид
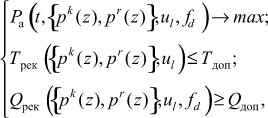(7)
где 
- время и точность выполнения задания процессором ПСКВ.
Для оценивания эффективности системного проектирования проведен сравнительный анализ синтезированного вычислительного устройства, использующего корректирующие способности кодов ПСКВ, с позиционным спецпроцессором ЦОС имеющим троированную мажоритарную структуру. В качестве исходных данных выбраны следующие параметры:
‒ разрядность кодирования (входного слова) - 31 бит;
‒ минимально допустимая разрядность входного слова - 11 бит;
‒ корректирующие способности устройства - обнаружение двукратных и исправление однократных ошибок.
Полученные результаты приведены на рисунке. Для удобства проведения анализа воспользуемся следующими сокращениями:
1 - вероятность безотказной работы разработанного СП ПСКВ;
2 - вероятность безотказной работы СП ПСС.
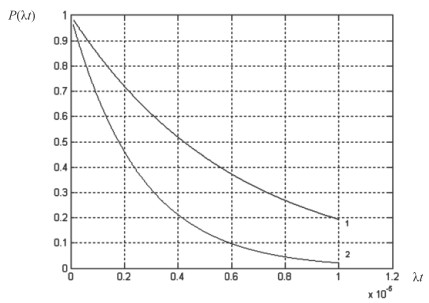
Сравнительная оценка отказоустойчивости СП ЦОС
Анализ зависимостей позволяет сделать следующие выводы. Применение системного проектирования позволило разработать специализированный процессор ЦОС класса вычетов, характеризующейся большей отказоустойчивостью по сравнению с позиционным вычислительным устройством цифровой обработки сигнала, реализующим метод маскирования отказов «2 из 3».
Список литературы
- Калмыков И.А. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа / И.А. Калмыков, Н.И. Червяков, Ю.О. Щелкунова, В.В. Бережной // Нейрокомпьютеры: разработка, применение. - 2003. - №6. - С. 61-68.
- Калмыков И.А. Высокоскоростные систолические отказоустойчивые процессоры цифровой обработки сигналов для инфотелекоммуникационных систем / И.А. Калмыков, А.В. Зиновьев, Я.В. Емарлукова // Инфокоммуникационные технологии. - 2009. - №2. - С. 31-37.
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов / под ред. Н.И. Червякова. - М: Физматлит, 2005. - 276 с.
- Анфилатов В.С. Системный анализ в управлении / В.С. Анфилатов, А.А. Емельянов, А.А. Кукушкин. - М.: Финансы и статистика, 2003. - 238 с.